Having introduced Joy in the previous post, as per our grand scheme of things, we are now ready for some coding.
As a first small project, I decided to try and implement a simple binary search tree. Nothing fancy, no self-balancing or anything evil like that. Just your Plain Old Binary Search Tree (which can be handily abbreviated as POBST).
The reason for this boring textbook example is twofold. First, Joy being, for me, a rather new way of thinking about code, I didn’t want to distract myself with something overly creative. Having a ready recipe for the thing I want to code provides me with a nice distraction-free, Joyful coding experience. Second, as Joy stresses function-level programming (no values and all that), I was wondering how a data structure, which I think of as a value, would look like in this paradigm.
(Source code for this post is in the repository).
First thing first, we need to have some representation of our tree. Now, we are quite far from our cozy OO land, mind you; we don’t even have simple structs in Joy. So this is your typical “we’re not in Kansas anymore” situation.
The omnipresent lists to the rescue. As we remember (or not), lists in Joy are heterogeneous, so we can stuff anything in them, including other lists, which fits well with the recursive nature of trees.
So for our tree, we’ll use a list with three elements – the first is the value, the second is the left subtree, and the third is the right subtree. All parts are optional. A couple of examples:
An empty tree
1
| |
A tree with a single node
1
| |
And this tree
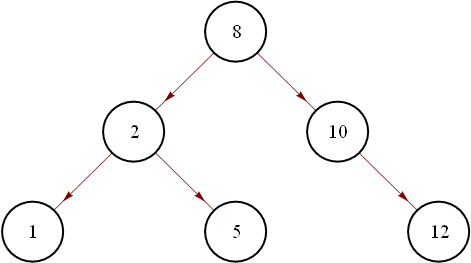
is
1
| |
Untangled all the brackets? Great, we can move on.
In view of how simple the tree representation is, the second reason for implementing binary trees kind of evaporates, oh well…
The full source code should be documented enough to be, in most parts, fairly readable; so I won’t be explaining it step by step here. The final result is rather boring, e.g., we can create and query a tree like this:
1
| |
(Note that, due to what I think is a bug in the interpreter, when adding a large number of items at a time, say 100, sometimes the interpreter either crashes or gives unexpected errors.)
No surprises here. But there are some interesting implementation details that are actually worth a discussion; we are getting to them below.
Having implemented getters (in a moment, we’ll see value, which extracts the value of a tree node), setters (as our trees are immutable, setters, or any mutating operations, actually produce new trees) and some predicates for the tree parts, I am getting to the interesting bits: adding and removing elements from the tree.
Adding an item to the tree is a simple recursive operation: traverse the tree till you find the right place, insert a new node with the value there. In case the item is already present, do nothing. Joy being Joy, we have a combinator that makes this possible without writing an explicitly recursive function. In this case, we use condlinrec (see manual), which performs linear recursion, but unlike linrec it can check for multiple conditions before the recursion step or stopping.
A skeleton for the adding function looks like something like this:
1 2 3 4 5 6 7 | |
It’s not that difficult to fill in the pseudocode bits, but we won’t be doing that; instead, let’s see what the deleting function should look like. In pseudocode:
1 2 3 4 5 6 7 | |
Hmm, rather similar, in both cases we are rebuilding the tree according to some value; the differences occur when we actually get to the value or when it’s missing. Being conscientious programmers, we cannot let this code duplication be. The code must be WET (which is like DRY, but more suitable for trees), and we must find a way to hydrate it.
Simple enough, this is a functional language; we can pass the appropriate handler functions as parameters and let them take care of the differences, while keeping common code intact:
1 2 3 4 5 6 7 8 9 10 | |
Great, we got ourselves WET with Joy, done; we can now move on to greener pastures.
Well, of course not, that was just pseudocode, we actually need an implementation for this thing. And here it is:
1 2 3 4 5 6 7 8 9 10 | |
Bugger me – I can’t quite read this, and I wrote that not that long ago.
So why is it so complicated? In the pseudocode above, I elided any references to argument handling; I just assumed the arguments to be there when needed. That’s quite natural for someone coming from a background of value-level programming languages. When you write a function, e.g., in Java, arguments to functions are just there, available, without any fuss, by their name. Not so when you’re dealing with a stack-based language; here, the arguments are implied to be on the stack, and they have no names. To be able to use them, you have to make sure that they are properly ordered on the top of the stack.
Back to our code. First, we have the easy bits; add-val and delete-val are actually quite similar to our pseudocode. They assume that a tree and a value to be added/removed are on top of the stack, each of them pushes their pair of handling functions onto the top of the stack, and passes control to build-tree-with-value.
The handler functions are rather simple; to figure them out, we need to remember that when we apply them we have the tree on the top of the stack and the value below it. After the application, we need to leave only the new tree and nothing else. I’ll leave the figuring out as an exercise to the reader (oh how I hate when people do that. At last, the oh so sweet revenge…).
Now, build-tree-with-value creates a function that takes three arguments: a tree, a value, and a list with a pair of handler functions; in that order, i.e. the handler functions are on the top of the stack. But we don’t want them that way, what we need is: handlers, value, tree. That’s what the first rollup swap functions do. After applying them, we are ready for the recursion. And that’s the last point where I can still explain the code without taking out a piece of paper and drawing many little stacks on it. As you can see, each condition is followed by a bunch of stack-manipulating functions, the whole purpose of which is to tweak the stack so that the arguments are in the right order, multiplicity and are ready for the further recursive calls. A horrid, horrid piece of code.
I would love to give the explanation of this code to you, the reader, as another exercise, but that would be just plain sadistic. And I won’t be bothered to explain it myself, that would be way too tedious, boring and quite meaningless. Why meaningless? Because by now, I think that it’s pretty clear that we are doing something wrong. To quote a comment from the The Joy of Concatenative Languages series
If you find you need to be continually aware of the stack, then, plain and simple, “You’re Doing It Wrong.”
We need to step back and see how we can alleviate the stack manipulation problem. To do that, we’ll examine a simpler case: the insert-at function. This function takes a list, a value and an index, and inserts the value at the specified position in the list. The algorithm we’ll be implementing is:
- take the first N – 1 items from the list (prefix)
- take the tail of list starting from the N + 1th item (tail)
- concatenate the prefix value and tail.
Simple enough, especially as we already have the take, drop and enconcat functions implemented for us. And here’s my first naive attempt at an implementation:
1 2 3 4 5 | |
Not the horrors of build-tree-with-value, but still far from satisfactory; we cannot, by any means, plead ignorance of the stack.
For the sport of it, let’s try to follow the definition.
- We start out with
list val index(the rightmost item is the top of the stack). - The first line rearranges it, so that we have
val list index list index. - The second line applies the
takefunction to the top two items and pushes the result down the stack, so we haveval prefix list index. - The third line calculates the tail of the list, leaving
val prefix tail. - The last line performs the concatenation of all three items on the stack, and we are done.
Now, our aim is to reduce the amount of stack related operations we see at each stage. To do this, I tried looking at the different functions and combinators available in Joy. But being a novice, I couldn’t find anything simple that makes the code much better. What I managed to figure out is that part of the complexity stems from the fact that in order to reuse an argument, I have to duplicate it on the stack, which requires even more manipulation of the stack. One of the combinators that I found, nullary, allows to use a function without removing its arguments from the stack, so one can avoid the duplication in that case. Here’s the best that I managed:
1 2 3 4 5 | |
The steps are as follows:
list val index–>val list indexval list index–>val list index prefix–>val prefix list indexval prefix list index–>val prefix tail- Concatenating the last three items.
A definite improvement, but I still don’t see it as a satisfactory result. The second line seems rather cryptic to me. Further investigation in this direction did not yield anything better, so I decided to leave it at that.
If there are any Joy or concatenative gurus reading this, I would love to hear your opinion on how this code can be improved.
After abandoning this direction, I had another idea. I will leave it till the next post in the series. But the upshot of it is that I was able to write the following code:
1 2 3 4 5 6 | |
Ignoring the surrounding splice-from-stack call, we’ve managed to remove all stack related manipulation. The cost, so it seems, is that we introduced something that looks like custom syntax.