class: center, middle, transition, intro # Compile Time Logic Programming <br /> in Scala ― What For? .centered.caption[Daniel Beskin] ??? - So, we're going to talk about doing logic-programming in Scala at compile-time --- ## Why? - Cleaner notation for compile-time computation - Helps read/write code that relies on implicits - Encode sophisticated invariants in types - Fun (?) ??? - This is actually not a new idea - And you might rightfully wonder, why would you want to do that? - As we'll see, we'll be able to use logic-programming as a cleaner notation for doing compile-time computation - Specifically, it should make it easier to read and write code that uses implicits - This is useful when either trying to learn various libraries, like Shapeless - Or when trying to write our own code with implicits - Since we'll be able to write fairly advanced compile-time code, **we'll be able to design complicated types** - **Types that will be able to capture sophisticated invariants about our code** - Ultimately, leading to more type-safety - Doing this "by hand" is difficult, but we will manage to get the compiler to help us construct these types - And if not all that, I at least hope that this will be fun - For some definition of "fun"... --- ## How? - A brief Prolog tutorial - Translation to implicits - Real World™ examples ??? - The plan for this talk is: - A quick introduction to Prolog, a language for logic programming - We'll use just the bare minimum that we'll need for our compile-time computations - After that I will show that the way Prolog works is similar to the way that Scala's implicits work - And so we'll use this fact to translate between Prolog and implicits - Then we'll move on to some, hopefully useful, examples of using this analogy between Prolog and implicits - **And I will do my best to avoid solving Sudoku as we go along** --- class: middle, transition, mostlyWrong .quote[> 1972 - Alain Colmerauer designs the logic language Prolog. His goal is to create a language with the intelligence of a two year old. He proves he has reached his goal by showing a Prolog session that says "No." to every query.] .footnote[― James Iry, "A Brief, Incomplete, and Mostly Wrong History of Programming Languages"] ??? - So Prolog is the most well known language for logic programming - This is a style of programming where we create a database of facts and rules - And then query this knowledge-base whether some fact or another is true - Where a typical Prolog answer to a question is: "no" - This style of programming can actually be quite useful in various domains - Like schedule-planning - **Though we will abuse it in a fairly special way** - Let's begin --- ## Prolog 101 - Facts ??? - The simplest thing we can do in Prolog is to state facts -- ```prolog hobbit(frodo). hobbit(bilbo). hobbit(primula). hobbit(mirabella). hobbit(belladonna). hobbit(hildbrand). hobbit(sigismond). hobbit(gerontius). ``` ??? - Here we are stating that `frodo`, `bilbo` and the others are Hobbits - Each fact is a value - In this case we have a compound value, or a functor (not to be confused with functors in Functional Programming) - The functor is called `hobbit` and it takes a single argument - The argument is an `atom`, and it can be any lower-case identifier - So the first fact can be read as `frodo` is a `hobbit` - Having declared some facts, we can query Prolog about them --- ## Prolog 101 - Facts ```prolog ?- hobbit(bilbo). {{content}} ``` ??? - The question mark means that we are in the REPL, where we can query the knowledege-base - In this case we are asking Prolog whether it is true that `bilbo` is a `hobbit` -- yes {{content}} ??? - And indeed it is - Prolog knows this fact since we stated it explicitly, so it confirms it -- ?- hobbit(gandalf). {{content}} ??? - We can ask other questions - In this case we are asking: is `gandalf` a `hobbit` -- no {{content}} ??? - Obviously not - Since we never stated this fact, there's no way that it can be true -- ?- hobbit(X). {{content}} ??? - Now we are using variables - Any upper-case identifier is a variable in Prolog - We are now asking: what are the values of `X` for which the statement "`X` is a `hobbit`" is true -- X = frodo X = bilbo X = primula X = mirabella X = belladonna X = hildbrand X = sigismond X = gerontius ??? - At this point Prolog will go over all known facts and will find the values of `X` that satisfy our query - We can have more sophisticated facts, for example --- ## Prolog 101 - Facts ```prolog parent(belladonna, bilbo). parent(primula, frodo). parent(mirabella, primula). parent(hildbrand, sigismond). parent(gerontius, mirabella). parent(gerontius, belladonna). parent(gerontius, hildbrand). ``` ??? - Now we are using a functor, `parent` that takes two arguments - This can be read as: `belladonna` is a `parent` of `bilbo` - And just like before, we can query the new knowledge-base --- ## Prolog 101 - Facts ```prolog ?- parent(primula, frodo). yes ?- parent(bilbo, frodo). no {{content}} ``` ??? - These are some simple queries, about facts that we stated - And the answers are what we expect - `primula` is the parent of `frodo` - But `bilbo` is not `frodo`'s parent - We can also use variables -- ?- parent(X, bilbo). X = belladonna {{content}} ??? - This asks: for what values of `X` it is true that `X` is the `parent` of `bilbo` - We can also ask the opposite question -- ?- parent(gerontius, X). X = mirabella X = belladonna X = hildbrand ??? - For what values of `X` it is true that `gerontius` is the parent of `X` - And Prolog finds three different answers - **So we see that the arguments of a fact are symmetric, we can query both of them in the same way** - Okay, so let's move on to rules --- ## Prolog 101 - Rules ```prolog grandparent(A, B) :- parent(A, C), parent(C, B). ``` ??? - A Prolog rule is some value, in this case `grandparent` - Followed by the colon-hyphen operator, that can be read as "if" - And then some facts - The meaning is that the left operand is true, if the right operand is true - In this example, we are saying: - `A` is a grandparent of `B` - If we can prove that `A` is a `parent` of `C` - And that `C` is the `parent` of `B` - So if we provide this rule with some values for `A` and `B` - Prolog will search all possible values of `C` and check whether these two conditions hold - If such a `C` is found, then `A` is a grandparent of `B` - Let's see some examples -- ```prolog ?- grandparent(gerontius, sigismond). yes ?- grandparent(bilbo, frodo). no {{content}} ``` ??? - In these cases we specify both `A` and `B` with two names - And Prolog tries to find some `C` that satisfies them - In the first case it succeeds, `gerontius` is a parent of `sigismond` - But it was not possible to prove that `bilbo` is a `grandparent` of `frodo` - As before, we can use variables when querying -- ?- grandparent(X, bilbo). X = gerontius. {{content}} ??? - So it is possible to derive, using the known facts and the `grandparent` rule, who is the `grandparent` of `bilbo` - As before, variables are symmetric -- ?- grandparent(gerontius, X). X = primula X = bilbo X = sigismond ??? - So we can find all of the grandchildren of `gerontius` - We can go even further --- ## Prolog 101 - Rules ```prolog ?- grandparent(X, Y). X = mirabella Y = frodo X = gerontius Y = primula X = gerontius Y = bilbo X = gerontius Y = sigismond ``` ??? - We can leave both arguments as variables - And now we get all of the grandparent/grandchild combinations known to the system - Prolog searches for them on its own - If we actually want to find out the relationship between `bilbo` and `frodo` - We'll need some more rules --- ## Prolog 101 - Rules ```prolog siblings(A, B) :- parent(C, A), parent(C, B). A \= B. first_cousin_once_removed(A, B) :- grandparent(C, B), siblings(C, D), parent(D, A). ``` ??? - Now we are defining what it means to be `siblings` - This can be read as: - `A` and `B` are siblings, - If there is some `C` - Such that `C` is the parent of both `A` and `B` - And `A` is not equal to `B` - In a similar manner, we can define being `first_cousin_once_removed` - This uses previously defined rules and facts - And if we query this rule -- ```prolog ?- first_cousin_once_removed(bilbo, frodo). yes {{content}} ``` ??? - We learn that `bilbo` is `frodo`'s `first_cousin_once_removed` - We can also list all of `frodo`'s known first cousins once removed -- ?- first_cousin_once_removed(X, frodo). X = bilbo X = sigismond ??? - So these are the very basics of Prolog - We'll need one more concept before we can move back to Scala - Lists --- ## Prolog 102 - Lists ```prolog [bilbo, frodo, primula] {{content}} ``` ??? - Lists are written with square brackets - And we can have queries with lists -- ?- member(bilbo, [bilbo, frodo, primula]). yes ?- member(belladonna, [bilbo, frodo, primula]). no {{content}} ??? - This asks whether the first argument is a `member` of the list in the second argument - We can also `append` lists -- ?- append([bilbo], [frodo, primula], Res). Res = [bilbo, frodo, primula] {{content}} ??? - This takes the lists in the first and second arguments and finds a value for the third argument, such that it equals to the concatenation of the two lists - But as we've seen so far, Prolog queries are symmetrical, so any argument can be a variable -- ?- append(Res, [primula], [bilbo, frodo, primula]). Res = [bilbo, frodo] ??? - Here the first argument is a variable - And now Prolog searches for a value of `Res` such that if it's concatenated to the second argument the result equals the third - So it subtracts one list from another - Which is nice, since we get multiple functions in a single relationship - We could also define these rules ourselves --- ## Prolog 102 - Lists ```prolog member(H, [H|T]). member(Elem, [H|T]) :- member(Elem, T). ``` ??? - Here we are using pattern matching on the arguments - The first fact pattern-matches on a list, using the pipe syntax, and breaks it into a head and a tail - We say that a value is present in a list, if the value and the head of the list are equal - The second pattern says that `Elem` is part of a list made of a head and a tail, if it is a member of the tail - So this will recursively go over the list and will actually work as we've seen on the previous slide - The `append` definition is somewhat mind-bending -- ```prolog append([], L, L). append([H|T], L1, [H|L2]) :- append(T, L1, L2). ``` ??? - In the first fact, we are saying that appending an empty list to another list results in the same list - The second rule says that if appending the tail of the first list to the second list `L1`, results in `L2` - Then appending the head and the tail of the first list to `L1` is the same as attaching the head of the first list to `L2` - It's hard to wrap your mind around this definition - But these three lines give us the powerful function from the previous slide - And that's pretty much all the Prolog we'll need for today - We can move to Scala now --- class: middle, transition .quote[> Any sufficiently advanced type-system is indistinguishable from Prolog.] .footnote[― The Curry-Howard correspondence, paraphrased] ??? - My aim now is to show you how similar Scala's type-system is to Prolog - Specifically, how programming with implicits is not that different from programming Prolog - And actually, the connection between type-systems and logic is very deep - But we won't be going into that now --- ## Implicits - Implicits are definitions that the compiler knows about - The compiler can use this knowledge to derive new knowledge - Much like Prolog searches for answers ??? - So, when we declare a Scala definition to be implicit - It becomes known to the compiler - When we ask the compiler to resolve a value implicitly - It will search, at compile-time, through all of the implicitly known definitions - And try to derive a value from them - This should sound familiar - Since it's quite similar to how Prolog works - Let's make the analogy more concrete by translating between the two --- ## Translation - Atoms vs. types .smallCode[`bilbo`] .smallCode[`trait Bilbo`] ??? - Prolog's atoms become simple Scala types -- - Compound terms vs. parameterized types .smallCode[`parent(X, Y)`] .smallCode[`trait Parent[X, Y]`] ??? - Compound terms that take arguments become types that take type-arguments - **So if a Prolog program runs over Prolog values, a Scala logic-program will run over types** - **That is, we are aiming at logic programming over the type-system** - Now we can state facts --- ## Translation - Facts vs. implicit values .smallCode[`parent(primula, frodo).`] .smallCode[`implicit val p: Parent[Primula, Frodo]`] ??? - A fact becomes an implicit definition - Which makes sense, because as I mentioned before, when we mark something implicit, the compiler gains knowledge about it - Just like the Prolog knowledge-base -- - Rules vs. chained implicits .smallCode[`siblings(A, B) :- ...`] .smallCode[`implicit def s\[A, B\](implicit ...): Siblings[A, B]`] ??? - The last part are rules - These become chained implicits - So to prove that `A` and `B` are siblings, we'll need some implicit definitions that tell us something about `A` and `B` - Now that we have both facts and rules, we can query them -- - Queries vs. implicit resolution .smallCode[`?- siblings(belladonna, mirabella).`] .smallCode[`implicitly[Siblings[Belladona, Mirabella]]`] ??? - Querying becomes a request for implicit resolution - When we ask for some implicit value, we force the compiler to search through its known implicits and come up with an answer - Just like Prolog - Let's see how we atually translate our hobbit example --- ## Translation in Practice ``` trait Frodo trait Bilbo trait Primula trait Mirabella trait Belladonna trait Hildbrand trait Sigismond trait Gerontius {{content}} ``` ??? - Since Scala is statically typed, we'll have to declare all of our types upfront - These are the "atoms" we'll use in our program -- trait Parent[A, B] trait Grandparent[A, B] trait Siblings[A, B] trait FirstCousinOnceRemoved[A, B] ??? - We'll also have to declare the possible compound terms - So we just mirror the Prolog ones, and give a type-parameter for each argument - Now we can actually declare some facts --- ## Translation in Practice - Facts ```prolog parent(belladonna, bilbo). parent(primula, frodo). parent(mirabella, primula). parent(hildbrand, sigismond). parent(gerontius, mirabella). parent(gerontius, belladonna). parent(gerontius, hildbrand). ``` ??? - We start with some Prolog code, and we'll translate it step by step - It's a pretty mechanical process, so it shouldn't be complicated - First step is capitalization an brackets --- ## Translation in Practice - Facts ``` Parent[Belladonna, Bilbo] Parent[Primula, Frodo] Parent[Mirabella, Primula] Parent[Hildbrand, Sigismond] Parent[Gerontius, Mirabella] Parent[Gerontius, Belladonna] Parent[Gerontius, Hildbrand] ``` ??? - Next we mark everything as implicit --- ## Translation in Practice - Facts ``` implicit val p1: Parent[Belladonna, Bilbo] implicit val p2: Parent[Primula, Frodo] implicit val p3: Parent[Mirabella, Primula] implicit val p4: Parent[Hildbrand, Sigismond] implicit val p5: Parent[Gerontius, Mirabella] implicit val p6: Parent[Gerontius, Belladonna] implicit val p7: Parent[Gerontius, Hildbrand] ``` ??? - **The names of the implicits don't mean anything for our logic program** - They are just noise that Scala requires us to write - We also need to provide some values for these definitions - But at the moment we don't really care about values, since we only want to operate on types - So we'll use dummy values --- ## Translation in Practice - Facts ``` implicit val p1: Parent[Belladonna, Bilbo] = new Parent[Belladonna, Bilbo] {} implicit val p2: Parent[Primula, Frodo] = new Parent[Primula, Frodo] {} implicit val p3: Parent[Mirabella, Primula] = new Parent[Mirabella, Primula] {} implicit val p4: Parent[Hildbrand, Sigismond] = new Parent[Hildbrand, Sigismond] {} implicit val p5: Parent[Gerontius, Mirabella] = new Parent[Gerontius, Mirabella] {} implicit val p6: Parent[Gerontius, Belladonna] = new Parent[Gerontius, Belladonna] {} implicit val p7: Parent[Gerontius, Hildbrand] = new Parent[Gerontius, Hildbrand] {} ``` ??? - And that's it, we've managed to state some facts to the Scala compiler - It's a bit noisy compared to Prolog, but it's good enough - Let's try convert a rule now - We start with the Prolog definition --- ## Translation in Practice - Rules ```prolog grandparent(A, B) :- parent(A, C), parent(C, B). ``` ??? - First, capitalization and brackets --- ## Translation in Practice - Rules ``` Grandparent[A, B] :- Parent[A, C], Parent[C, B]. ``` ??? - Now we reverse the 'if' operator and rename it to `implicit` --- ## Translation in Practice - Rules ``` (implicit Parent[A, C], Parent[C, B]): Grandparent[A, B] ``` ??? - This almost looks like Scala - So we just add what's necessary to make it a legal definition --- ## Translation in Practice - Rules ``` implicit def grandparent[A, B, C] (implicit p1: Parent[A, C], p2: Parent[C, B]): Grandparent[A, B] ``` ??? - That's even more noise - But once again, the name of the definition is meaningless - We also have to declare all our variables upfront - **Still, if you squint hard enough it resembles the Prolog rule we started with** - To complete the definition we'll provide a dummy value --- ## Translation in Practice - Rules ``` implicit def grandparent[A, B, C] (implicit p1: Parent[A, C], p2: Parent[C, B]): Grandparent[A, B] = new Grandparent[A, B] {} ``` ??? - This completes the rule - And now we can query our knowledge-base --- ## Translation in Practice - Queries <!--- Using 'asciidoc' rather than 'text' because gives the correct indentation, but with minimal highlighting. ---> ```asciidoc scala> implicitly[Parent[Belladonna, Bilbo]] {{content}} ``` ??? - We are asking the compiler: is it true that `Belladona` is the `Parent` of `Bilbo`? -- ​res0: Parent[Belladonna,Bilbo] = $anon$1@2440446 {{content}} ??? - And that's the result - The compiler found a value of the right type for us - This is equivalent to Prolog answering `yes` - Not succinct, but gets the point across - We can make a failing query -- scala> implicitly[Parent[Bilbo, Frodo]] ^ error: could not find implicit value for parameter e: Parent[Bilbo,Frodo] ??? - This time we fail to compile - Which means that there isn't an implicit value that matches this type - So a compilation error is equivalent to Prolog's `no` - We can also query rules --- ## Translation in Practice - Queries ```asciidoc scala> implicitly[Grandparent[Mirabella, Frodo]] res1: Grandparent[Mirabella,Frodo] = $anon$8@6d561529 scala> implicitly[Grandparent[Mirabella, Bilbo]] ^ error: could not find implicit value for parameter e: Grandparent[Mirabella,Bilbo] {{content}} ``` ??? - It works as expected, assuming that we convert successful compilation to `yes`, failed compilation to `no` - But what if we want to make a query with a variable? - Naively, we can try something like this: -- scala> implicitly[Grandparent[Mirabella, _]] {{content}} -- ​res2: Grandparent[Mirabella, _] = $anon$8@74a742ff ??? - We've placed a wildcard for the variable - And it compiles - But the resulting type doesn't actually contain an answer - It just uses the same wildcard - What the compiler is saying is: yes there is a value that matches our query - But its type matches `Grandparent[Mirabella, _]` - So that's what it gives us - Which means that we have a problem - We don't really have a straightforward way to tell Scala: - Set one type-parameter but infer the other - This is the first point where we start diverging from Prolog - But it's possible to circumvent this issue - Like so --- ## Translation in Practice - Complications ``` def findGrandchild[A, B] (a: A) (implicit gp: Grandparent[A, B]): Grandparent[A, B] = gp ``` ??? - We define a helper method - The helper takes a value of type `A` - And asks the compiler to derive an implicit for `Grandparent` of `A` and `B` - By providing an `A` value, the compiler infers the right type for `A` - But we leave the `B` type unspecified, which forces the compiler to infer it for us - **So we've broken Prolog's argument symmetry** - But it works -- ```asciidoc scala> findGrandchild(new Mirabella {}) res4: Grandparent[Mirabella,Frodo] = $anon$8@4e379d48 ``` ??? - The compiler derived the `Frodo` type for us - Though we are forced to provide a dummy value for `Mirabella` - So this allows us to find the grandchildren - If we want to do the opposite and find a grandparent - We'll need another helper -- ``` def findGrandparent[A, B] (b: B) (implicit gp: Grandparent[A, B]): Grandparent[A, B] = gp ``` ??? - Here we are specifying the `B` type, and leave `A` to be inferred by the compiler - We can compile -- ```asciidoc scala> findGrandparent(new Frodo {}) ^ error: could not find implicit value for parameter gp: Grandparent[A,Frodo] ``` ??? - And it doesn't work - Which might seem strange, but it has a reasonable explanation --- ## Translation in Practice - Complications ``` implicit def grandparent[A, B, C] (implicit p1: Parent[A, C], p2: Parent[C, B]): Grandparent[A, B] = new Grandparent[A, B] {} ``` ??? - The type parameters in our rule are resolved from left to right - So when we search for the grandparent of `Frodo`, we first need to have an implicit `Parent[A, C]` - But at this point we don't know `A` and `C` - And so all `Parent` implicits are valid - This means we have an ambiguous implicit, and the search fails - But we can work around this limitation by adding another rule -- ``` implicit def grandparent2[A, B, C] (implicit p1: Parent[C, B], p2: Parent[A, C]): Grandparent[A, B] = new Grandparent[A, B] {} ``` ??? - It's a small variation on the original rule - It just swaps the order of the arguments - This first implicit infers the parent of `Frodo` which is unique - And only then proceeds searching for the grandparent, which is again unique - So we restore back the symmetry we had in the original Prolog definition - And now it works - (Though note that this adds some ambiguity to some of our previous queries) - (To solve it, we'll need to play around with implicit resolution priority, see the repo) -- ```asciidoc scala> findGrandparent(new Frodo {}) res7: Grandparent[Mirabella,Frodo] = $anon$9@3e27f24a ``` ??? - But what if we have multiple grandchildren? --- ## Translation in Practice - Complications ```asciidoc scala> findGrandchild(new Gerontius {}) ^ error: could not find implicit value for parameter gp: Grandparent[Gerontius,B] ``` ??? - It fails to compile - But not because there aren't any grandchildren - It's because there is more than one grandchild - At some point in the implicit resolution chain we hit an ambiguous implicit and the whole thing fails - **This is a serious limitation compared to Prolog, where we naturally handle any number of results** - **And it significantly limits the kind of problems we can solve with our compile-time Prolog** - **Won't stop us trying though...** - Let's move on to lists --- ## Translation - Lists - If Prolog values are types - Then Prolog lists are lists of types - HLists ??? - As we've seen, Prolog values are types in Scala - This means that a list of Prolog values is a list of Scala types - And we have a name for such a thing - An `HList`, that is a heterogeneous list - Which you can think of as tuples of any length - Let's see how we define them --- ## Translation - Lists ``` sealed trait HList case class ::[H, T <: HList](head: H, tail: T) extends HList case object HNil extends HList ``` ??? - This mimics the definition for regular lists - We have a case for an empty list: `HNil` - And for a list made of a head and a tail, the double colon - But now we have more types - The non empty list actually has types for both the head and the rest of the list - It will be easier to follow with an example -- ``` scala> 1 :: true :: "abc" :: HNil res5: Int :: Boolean :: String :: HNil = 1 :: true :: abc :: HNil ``` ??? - We have a list with three values - Each value has its own type - And each type is recorded in the type of the result - So it's actually a list of types - **Notice how the values mimic the types** - **That's a very common pattern when doing type-level programming** - And will be useful later on - Just like in Prolog, we can perform actions with our lists --- ## Translation - Lists ``` sealed trait Member[Elem, L <: HList] sealed trait Append[L1 <: HList, L2 <: HList, R <: HList] ``` ??? - These are the types that allow us to check whether a list contains some member and to append lists - We can implement the same rules for them as the ones that we've seen for the Prolog equivalents - The translation mimics them exactly - But I'll skip their implementation for now, and you can see the full code in the repo for this presentation --- class: middle, transition .quote[> ― And in fact it turns out we have Prolog in our     type checker! ― Intentionally, or...? ― Well, it turns out it was a fortuitous coincidence.] .footnote[― Martin Odersky, Future-proofing Scala collections] ??? - Now we are ready for some real-world examples - As you can see from the quote, this probably wasn't intended to begin with - But it's actually quite amazing what we can achieve with our newfound Prolog powers - So where do we begin in our real-world? --- ## Sudoku ??? - Prolog is very good at solving puzzles - Sudoku being a classic example of this - And we can actually implement sudoku in the type-system -- .no[no] ??? - But we won't - **Because no matter how much I tried, I couldn't find any real-world use for sudoku** - **In the type-system, or anywhere else** - So let's move to something else --- ## CanBuildFrom "The longest suicide note in history?" ??? - Anyone who worked with Scala's 2.8 collections probably saw `CanBuildFrom` at one point or another - It can look somewhat intimidating - Even earning the title of being a suicide note - But viewed as a Prolog program, it's actually not that scary - The actual definition of `CanBuildFrom` is this -- ``` trait CanBuildFrom[-From, -Elem, +To] { def apply(from: From): Builder[Elem, To] } ``` ??? - So a `CanBuildFrom` instance provides the means to actually build a value of of some target collection, `To` - Using elements of type `Elem`, starting from a type `From` - But we don't actually want to provide our own `CanBuildFrom` instances - So we'll need some implicits --- ## CanBuildFrom ``` implicit def bf1[A, B]: CanBuildFrom[List[A], B, List[B]] implicit def bf2[A, B]: CanBuildFrom[Set[A], B, Set[B]] implicit def bf4[A, B]: CanBuildFrom[BitSet, Int, BitSet] implicit def bf3[A, B]: CanBuildFrom[BitSet, B, Set[B]] implicit def bf5[A, B](implicit o: Ordering[B]) : CanBuildFrom[SortedSet[A], B, SortedSet[B]] ``` ??? - So this is a sample of some implicit `CanBuildFrom` that we can have - This is quite noisy, but as a Prolog program it's quite simple --- ## CanBuildFrom ```prolog can_build_from(list(A), B, list(B)). can_build_from(set(A), B, set(B)). can_build_from(bit_set, int, bit_set). can_build_from(bit_set, B, set(B)). can_build_from(sorted_set(A), B, sorted_set(B)) :- ordering(B). ``` ??? - So - For any `B`, we can build a list of `B` from a list of `A` - Same goes for sets - Bit-sets are trickier - We can build bit-sets from `Int`s - But for any other type `B`, we can only build a regular set of `B` - Building sorted-sets requires a rule - We can only build a sorted set of `B` if we have an ordering for `B` - In this form it's quite readable - And if it was just that, I don't think that the hatred for `CanBuildFrom` would be so intense - The problem is that the Scala 2.8 collection hierarchy is quite big --- ## CanBuildFrom .collectionsHierarchy[] ??? - This is just a sample from the hierarchy - Implicits for `CanBuildFrom` can reside anywhere in this tree - So yes, this is a simple Prolog program, but it's spread over way too many files for us to be able to easily figure it all out --- ## Typeclasses ??? - Our next example is typeclasses - They are a very useful pattern in Scala - I won't go into its details - We'll just look at them from the Prolog point of view -- ``` trait CanWrite[A] { def write(value: A): Json } ``` ??? - This is a typeclass that asserts that `A` can be written to JSON - And we have a corresponding value-level method that converts an `A` value to a JSON value - We can state some facts about this --- ## Typeclasses ```prolog can_write(string). can_write(int). {{content}} ``` ??? - We can write `string`s and `int`s -- can_write(list(A)) :- can_write(A). can_write(option(A)) :- can_write(A). {{content}} ??? - The first rule says that given that we can write an `A` we can also write a list of `A` - The second rule says the same for options. -- can_write(tuple(A, B)) :- can_write(A), can_write(B). {{content}} ??? - Similarly, we can write a tuple of `A` and `B` if we can write both `A` and `B` - And we can query this knowledge, for example: -- ?- can_write(list(option(tuple(string, int)))). yes ??? - Prolog managed to derive that the given rules and facts imply that we can also write a list of an option of a tuple of a string and an int - Now let's go back to Scala --- ## Typeclasses ```prolog can_write(string). can_write(int). can_write(list(A)) :- can_write(A). can_write(option(A)) :- can_write(A). can_write(tuple(A, B)) :- can_write(A), can_write(B). ``` ??? - We start from the Prolog definitions, and mechanically translate to Scala - First, capitalization --- ## Typeclasses ``` CanWrite[String] CanWrite[Int] CanWrite[List[A]] :- CanWrite[A]. CanWrite[Option[A]] :- CanWrite[A]. CanWrite[Tuple[A, B]] :- CanWrite[A], CanWrite[B]. ``` ??? - Now we mark facts as implicit --- ## Typeclasses ``` implicit CanWrite[String] implicit CanWrite[Int] CanWrite[List[A]] :- CanWrite[A]. CanWrite[Option[A]] :- CanWrite[A]. CanWrite[Tuple[A, B]] :- CanWrite[A], CanWrite[B]. ``` ??? - Convert the rules by reversing them and marking as implicit --- ## Typeclasses ``` implicit CanWrite[String] implicit CanWrite[Int] (implicit CanWrite[A]): CanWrite[List[A]] (implicit CanWrite[A]): CanWrite[Option[A]] (implicit CanWrite[A], CanWrite[B]): CanWrite[Tuple[A, B]] ``` ??? - And now complete to full Scala definitions --- ## Typeclasses ``` implicit val canWriteString: CanWrite[String] implicit val canWriteInt: CanWrite[Int] def canWriteList[A] (implicit canWriteA: CanWrite[A]): CanWrite[List[A]] def canWriteOption[A] (implicit canWriteB: CanWrite[A]): CanWrite[Option[A]] def canWriteTuple[A, B] (implicit canWriteA: CanWrite[A], canWriteB: CanWrite[B]): CanWrite[Tuple[A, B]] ``` ??? - Again, the names don't really matter, it's just the syntax that Scala forces us to use - What's missing are the values - Previously we just used dummies - But now we'll do something more useful - We'll actually implement the value-level behavior - For example --- ## Typeclasses ``` implicit val canWriteString: CanWrite[String] = new CanWrite[String] { def write(value: String) = JsString(value) } {{content}} ``` ??? - We convert a `String` value by wrapping it into a JSON constructor -- implicit def canWriteList[A] (implicit canWriteA: CanWrite[A]): CanWrite[List[A]] = new CanWrite[List[A]] { def write(values: List[A]) = JsArray { values.map(aValue => canWriteA.write(aValue)) } } ??? - For lists we need something more complicated - Here we map over the input values - And use the provided `CanWrite` instance for `A` to convert these values into JSON - We then wrap the whole thing into a JSON array - We can do something similar for the other definitions - Once we do that, we can query the compiler --- ## Typeclasses ```asciidoc scala> val canWrite = implicitly[CanWrite[List[Option[(String, Int)]]]] canWrite: CanWrite[List[Option[(String, Int)]]] = CanWrite$$anon$4@9b1dda0 {{content}} ``` ??? - Just like in the Prolog code - The compiler managed to deduce that it's possible to write a list of option of a tuple of a `String` and `Int` - But that's not all - It provided us with a value - Since we were careful to implement our `CanWrite` instances properly - We can now actually use this instance -- scala> canWrite.write(List(Some("a", 1), None)) res6: Json = [["a", 1], null] ??? - Which actually work for values - **So we've managed to tie our type-level computation to a useful value-level result** - **The code for this `CanWrite` instance is something that we didn't have to write** - We just taught the compiler some rules and it managed to derive it for us - This is something that happens a lot when using typeclasses - **And tracing the process with Prolog can sometimes help in figuring out what's happening** - We are now ready for our last example --- ## Akka Streams Graphs ??? - How many people here are familiar with Akka Streams? - Okay - I won't actually go into any details about Akka Streams - But just use one high-level concept from it -- .streamFlow[] ??? - One of the things that Akka Streams lets us do is to describe data-flow graphs - Like this one - We have some source of data - That we broadcast into two flows - Then we merge them - And stream the results into a sink - The various `f`s here stand for flows - They can potentially modify the incoming data - Starting from this diagram, Akka Streams provides us with a DSL that allows us to convert it into code --- ## Akka Streams Graphs ``` val graph = GraphDSL.create() { implicit builder: GraphDSL.Builder[NotUsed] => {{content}} ``` .graphBrace[```}```] ??? - We start with some boilerplate - Which I won't be explaining now -- val in = Source(1 to 10) val out = Sink.foreach(println) {{content}} ??? - Next we declare source and a sink - One produces values - The other consumes them -- val bcast = builder.add(Broadcast[Int](2)) val merge = builder.add(Merge[String](2)) {{content}} ??? - Next we have our broadcast and merge components -- val f1 = Flow[Int].map(_ * 2) val f2 = Flow[Int].map(_.toString ++ "!") val f3 = Flow[String].map(s => "*" ++ s ++ "*") val f4 = Flow[Int].map(_.toString ++ "?") {{content}} ??? - Now some flows, each flow applies a function to its inputs - For example, the second flow take an `Int` and produces a `String` - And now we can actually build our graph -- in ~> f1 ~> bcast ~> f2 ~> merge ~> f3 ~> out bcast ~> f4 ~> merge {{content}} ??? - This syntax is meant to be a straightforward translation from our diagram - It actually looks quite nice - It's not that hard to follow and translate back into a diagram - But we are not done yet -- ClosedShape ??? - This tells the DSL that we are dealing with a closed shape - That is, each port in every stage is connected to exactly one other port - And this bothers me - This is just an assertion, not a proven fact - Suppose we forget to connect some ports - If we run such a graph --- ## Akka Streams Graphs ```asciidoc scala> graph.run() java.lang.IllegalStateException: Illegal GraphDSL usage. Inlets [Merge.in1] were not returned in the resulting shape and not connected. Outlets [Map.out] were not returned in the resulting shape and not connected. at akka.stream.scaladsl.GraphDSL$Builder... ... ``` ??? - We fail at runtime with an exception - So we just asserted something and it wasn't checked until run-time - **But that's exactly what we have types for, to catch these things at compile-time** --- ## Type-safety - We want a `ClosedShape` that cannot fail - Each value of `ClosedShape` has all of its ports connected - Constructing values "by hand" is difficult - But the compiler can do it for us ??? - What we really want is a type-safe `ClosedShape` - Such that if we build a graph from it and it compiles, it can never fail at runtime - But imagine that type - How will you encode such a complicated invariant? - **Constructing values of something like this "by hand" is difficult** - But now that we know Prolog, we can make the compiler do it for us - A Prolog program that proves that a shape is closed is actually not that complicated - So we'll write it and then convert it into implicits - This should bring back type-safety --- ## Closed-shape Prolog ```prolog in(sink, 1, string). in(broadcast, 1, int). in(merge, 1, string). in(merge, 2, string). in(flow1, 1, int). in(flow2, 1, int). in(flow3, 1, string). in(flow4, 1, int). out(source, 1, int). out(broadcast, 1, int). out(broadcast, 2, int). out(merge, 1, string). out(flow1, 1, int). out(flow2, 1, string). out(flow3, 1, string). out(flow4, 1, string). ``` ??? - We start by declaring the various ports - An `in` takes a stage, a port number and the type that it can consume - So the first line here reads as: The `sink` stage has an inlet, numbered 1 that consumes `string`s - Similarly for `out` - So the `source` stage has an outlet, numbered 1 that produces an `int` - Next we want to connect the various inlets and outlets --- ## Closed-shape Prolog ```prolog connect(out(source, 1, int), in(flow1, 1, int)). connect(out(flow1, 1, int), in(broadcast, 1, int)). connect(out(broadcast, 1, int), in(flow2, 1, int)). connect(out(broadcast, 2, int), in(flow4, 1, int)). connect(out(flow2, 1, string), in(merge, 1, string)). connect(out(flow4, 1, string), in(merge, 2, string)). connect(out(merge, 1, string), in(flow3, 1, string)). connect(out(flow3, 1, string), in(sink, 1, string)). ``` ??? - A `connect` takes an `out` and an `in` and connects them - So the first lines says that the `source`'s outlet is connected to `flow1`s inlet - And similarly for the rest of the connections - Before we can prove that the shape is closed, we'll need some helpers --- ## Closed-shape Prolog ```prolog all_ports_for_stage(Stage, AllPorts) :- find_all(in(Stage, _, _), InPorts), find_all(out(Stage, _, _), OutPorts), append(InPorts, OutPorts, AllPorts). ``` ??? - This rule lets us compute all of the ports that are associated with a stage - The `find_all` rule finds all of the values of the variables on the left argument that make the value here true - And it then places them in the second argument as a list of results - So for a given `Stage` we collect all of its inlets and outlets - Then we append them into a single list called `AllPorts` - For example: -- ```prolog ?- all_ports_for_stage(broadcast, Ports). Ports = [ in(broadcast,1,int), out(broadcast,1,int), out(broadcast,2,int) ] ``` ??? - We can find all the ports for the `broadcast` stage and put it in the `Ports` variable --- ## Closed-shape Prolog ```prolog all_ports([], []). all_ports([H|T], Result) :- all_ports_for_stage(H, HeadPorts), all_ports(T, TailPorts), append(HeadPorts, TailPorts, Result). ``` ??? - Next we have a rule that collects all the ports for a list of stages - For an empty list it's empty - Otherwise, we collect the ports of the head and append them to the ports of the tail - And it works like this -- ```prolog ?- all_ports([source, flow1], Ports). Ports = [ out(source,1,int), in(flow1,1,int), out(flow1,1,int) ] ``` ??? - Now we can start defining the closed-shape rule --- ## Closed-shape Prolog ```prolog closed_shape([], _). {{content}} ``` ??? - The closed-shape rule takes two arguments - The first is a list of ports to check - And the second is the full list of ports we have in our system - In case we don't have any ports to check, the shape is definitely closed -- closed_shape([Out|T], AllPorts) :- Out = out(_, _, Type), In = in(_, _, Type), exactly_once(connect(Out, In)), member(In, AllPorts), closed_shape(T, AllPorts). {{content}} ??? - Next we look at a non-empty list of ports to check - This rule applies when the head of the list is an outlet - In which case we try to find an inlet that has a matching type - And that connects to this outlet - We wrap with an `exactly_once` call, since we want to make sure that we never connect the same outlet to multiple inlets - Then we verify that the inlet we found is a member of the full list of ports - As we don't want to accidentally connect to an external port - Then we verify that the tail is a closed-shape -- closed_shape([In|T], AllPorts) :- In = in(_, _, Type), Out = out(_, _, Type), exactly_once(connect(Out, In)), member(Out, AllPorts), closed_shape(T, AllPorts). {{content}} ??? - We now have another rule that swaps the roles of the outlet and the inlet - But otherwise is exactly the same - We'll add a last rule, just to make it nicer to use -- closed_shape(Stages) :- all_ports(Stages, AllPorts), closed_shape(AllPorts, AllPorts). ??? - We are overloading `closed_shape`, so it can work directly with stages - So a list of stages is closed if all of its ports are closed - And we generate the list of all ports with the `all_ports` rule - And then pass on the result to the original `closed_shape` rule - And we're done --- ## Closed-shape Prolog ```prolog ?- closed_shape( [source, sink, merge, broadcast, flow1, flow2, flow3, flow4] ). yes {{content}} ``` ??? - Now we can verify that our stages actually form a closed shape -- ?- closed_shape( [source, sink, merge, broadcast, flow1, flow3, flow4] ). no ??? - But we can now also detect shapes that are not closed - With this code as inspiration, we are now ready to solve this problem in Scala --- ## Closed-shape Implicits ``` sealed trait Port trait `1` extends Port trait `2` extends Port {{content}} ``` ??? - First we declare our types upfront - These are just the port numbers -- trait Stage {{content}} ??? - A type for stages -- case class In[-S <: Stage, -P <: Port, A](inlet: Inlet[A]) case class Out[-S <: Stage, -P <: Port, A](outlet: Outlet[A]) {{content}} ??? - The `In` type stands for an inlet for some stage and some port and an incoming type - Since we'll eventually need values, we actually wrap a real `Inlet` value - And we do the same thing for outlets -- case class Connect[O <: Out[_, _, A], I <: In[_, _, A], A](o: O, i: I) ??? - The `Connect` type stands for a connection between an outlet and an inlet of matching types - At this point, in the Prolog program we defined a rule to find all of the ports of a stage - But with implicits we have a problem - **Implicits can't resolve multiple values for a single invocation** - So we can't write this rule - Instead, we'll have to compromise and specify the ports directly on our stages --- ## Closed-shape Implicits ``` trait Stage { type Ports <: HList } ``` ??? - We are now saying that each `Stage` has an associated list of ports - Now we can write a rule to find all of the ports for a list of stages --- ## Closed-shape Implicits ``` sealed trait AllPorts[Stages <: HList, Ports <: HList] {{content}} ``` ??? - So given a list of `Stages` we'd like the `Ports` list to contain all of the ports associated with that list -- implicit val portsOfEmpty: AllPorts[HNil, HNil] = new AllPorts[HNil, HNil] {} {{content}} ??? - We pretty much follow the Prolog definition - An empty list of stages has an empty list of ports -- implicit def portsOfList[S <: Stage, StagesTail <: HList, PortsTail <: HList, Result <: HList] (implicit tailPorts: AllPorts[StagesTail, PortsTail], append: Append[S#Ports, PortsTail, Result]) : AllPorts[S :: StagesTail, Result] = new AllPorts[S :: StagesTail, Result] {} ??? - Now we have a rule for a non-empty list - The signature is scary, but try to keep the Prolog code in mind - So given all of the ports for the tail of the stages list - We can append the head's ports to the ports of the tail - This gives the ports for the complete list - Now we can define our `ClosedShape` type --- ## Closed-shape Implicits ``` sealed trait ClosedShape[Ports <: HList, AllPorts <: HList] { def connections: List[Connect[_, _, _]] } {{content}} ``` ??? - This type asserts that the first ports list forms a closed shape within the full ports list - But since we want to construct an actual graph of values in the end - We now add a method that produces the list of connections for those ports - What we want is that every instance of this type is going to produce a valid graph - That is, if we construct a graph from the list of `Connect`s of a `ClosedShape` it can never fail at runtime - And our Prolog program is going to enforce this and build the list for us -- implicit def emptyConnected[AllPorts <: HList] : ClosedShape[HNil, AllPorts] = new ClosedShape[HNil, AllPorts] { def connections = Nil } ??? - So an empty list is a closed-shape - Next, the case of a non-empty list --- ## Closed-shape Implicits ``` implicit def outFirst[O <: Out[S, P, _], I <: In[_, _, _], S <: Stage, P <: Port, PortsTail <: HList, AllPorts <: HList] (implicit headConnection: Connect[O, I, _], member: Member[I, AllPorts], tailClosedShape: ClosedShape[PortsTail, AllPorts]) : ClosedShape[O :: PortsTail, AllPorts] = new ClosedShape[O :: PortsTail, AllPorts] { def connections = headConnection :: tailClosedShape.connections } ``` ??? - This is probably the scariest piece of code till now - But it's very similar to our original Prolog code - If the head of the list is an outlet - We find its connection to some inlet - Verify that it's a member of the full list of ports - And then verify that the tail of the list is closed as well - This proves that the whole list is a closed-shape - **The main difference between the Prolog version and this one is that we don't have to invoke the `exactly_once` function** - Since Scala's implicits can only be resolved once or not at all - We are also careful to implement the `connections` method with the correct value - Notice how it mimics the type-level computation by adding the head to the tail here - We'll need similar code for an inlet at the head - But I'll skip it, since it's almost the same - We wrap up with a function that connects everything --- ## Closed-shape Implicits ``` def build[Stages <: HList, Ports <: HList] (stages: Stages) (implicit allPorts: AllPorts[Stages, Ports], closedShape: ClosedShape[Ports, Ports]) : AkkaClosedShape = { def makeConnection[A](c: Connect[_, _, A]): Unit = c.out.outlet ~> c.in.inlet val connections = closedShape.connections.toSet connections.foreach(c => makeConnection(c)) AkkaClosedShape } ``` ??? - Given a list of stages - We find all of their ports - And then prove that they form a closed-shape - This gives us an instance of `ClosedShape` - Which we can now use to join the actual inlets and outlet - After we've done that, we can safely assert that the shape we now have is closed - So we've converted our compile-time proof into an actual value we can use --- ## It Compiles, Ship It! ``` val source = Source() val sink = Sink() val broadcast = Broadcast() val merge = Merge() val flow1 = Flow1() val flow2 = Flow2() val flow3 = Flow3() val flow4 = Flow4() ``` ??? - And after some more wiring, which I'll skip - We get to the code that actually runs everything - We create the various stages --- ## It Compiles, Ship It! ``` implicit val c1: Connect[Source#Out1, Flow1#In1, Int] = Connect(source.out1, flow1.in1) implicit val c2: Connect[Flow1#Out1, Broadcast#In1, Int] = Connect(flow1.out1, broadcast.in1) implicit val c3: Connect[Broadcast#Out1, Flow2#In1, Int] = Connect(broadcast.out1, flow2.in1) implicit val c4: Connect[Broadcast#Out2, Flow4#In1, Int] = Connect(broadcast.out2, flow4.in1) implicit val c5: Connect[Flow2#Out1, Merge#In1, String] = Connect(flow2.out1, merge.in1) implicit val c6: Connect[Flow4#Out1, Merge#In2, String] = Connect(flow4.out1, merge.in2) implicit val c7: Connect[Merge#Out1, Flow3#In1, String] = Connect(merge.out1, flow3.in1) implicit val c8: Connect[Flow3#Out1, Sink#In1, String] = Connect(flow3.out1, sink.in1) ``` ??? - We state the facts about what is connected to what --- ## It Compiles, Ship It! ``` val allStages = source :: sink :: broadcast :: merge :: flow1 :: flow2 :: flow3 :: flow4 :: HNil ClosedShape.build(allStages) ``` ??? - Now we gather all of our stages - And build the shape - And it compiles - Which is now guaranteed to be runnable - On the other hand -- ``` val allStages = source :: sink :: broadcast :: merge :: flow1 :: flow2 :: flow3 :: HNil ClosedShape.build(allStages) ``` ??? - If we miss some connections, in this case `flow4` -- ```asciidoc ClosedShapeApp.scala:49: could not find implicit value for parameter closedShape: ClosedShape[Ports,Ports] ClosedShape.build(allStages) ^ ``` ??? - It fails to compile, just like we wanted to - As we've managed to regain type-safety, this completes the example --- ## Debugging ??? - You may be thinking now: we are actually writing some non-trivial code that runs at compile-time - This is an actual program - What happens if it doesn't work - Can we debug it? -- .no[no] ??? - I mean, it's not impossible to debug implicit resolution - But it's quite difficult --- ## Debugging - `-Xlog-implicits` - The [splain](https://github.com/tek/splain) compiler plugin - IntelliJ's "implicit hints" ??? - We can use the `Xlog-implicits` compiler flag - Which just prints everything that happens during implicit resolution - But the output is not easy to read - There's also the splain compiler plugin - Which attempts to prettify the output - IntelliJ's Scala plugin has support for showing implicits directly in the source code - This can be very useful and may help navigating the implicit call chain - All of these things can help to some extent - But it still remains quite difficult to really debug anything - For example --- ## Debugging .logImplicits[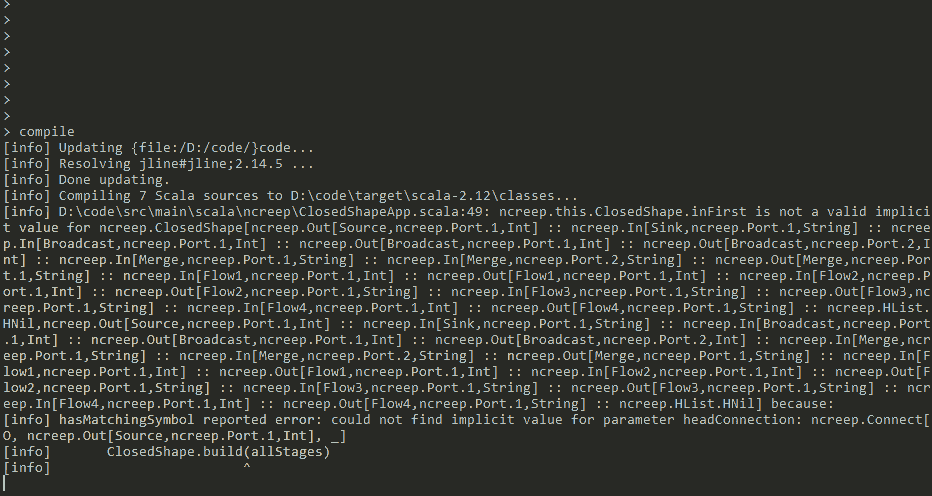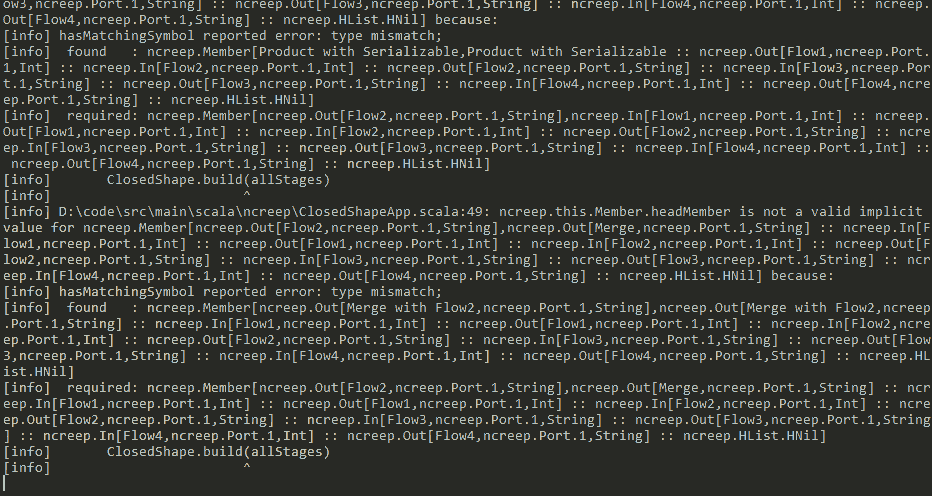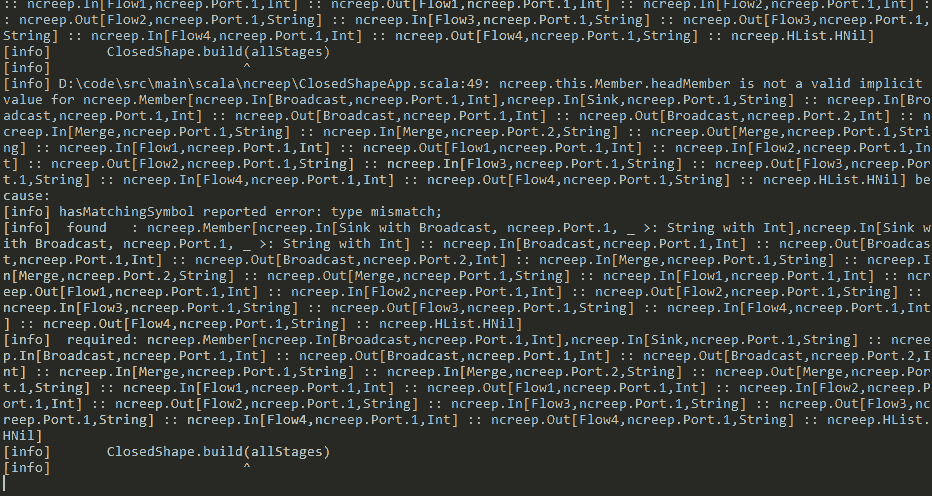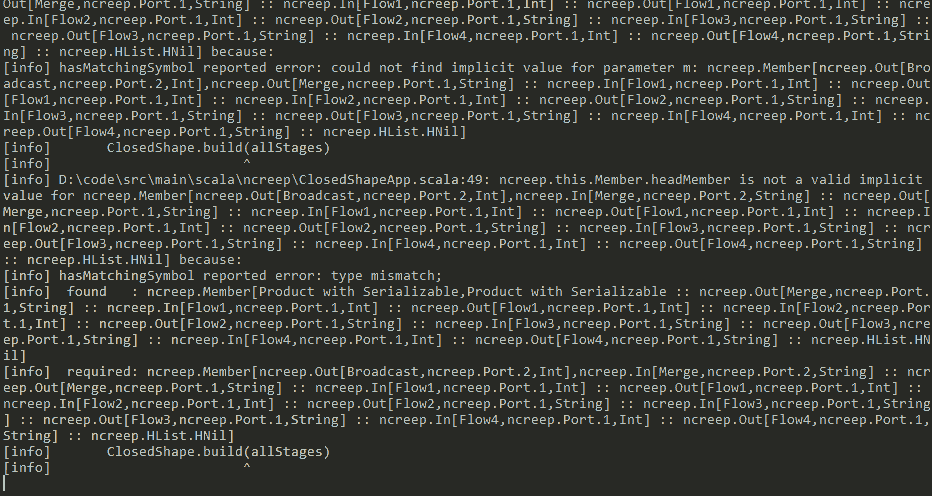] ??? - This is what the output from `Xlog-implicits` looks like for our last example - Good luck following that... --- ## Conclusion - Scala's implicits are a lot like Prolog - Using Prolog, it can be easier to follow implicits - Either in libraries or your own code ??? - So we've seen how implicit resolution is a lot like Prolog - And that we can use this similarity to better understand code that uses impilcits - Like the usage of typeclasses, which is pretty widespread these days - **By using Prolog as a notation for type-level programming, we can make these programs easier to follow** - And you can use these skills either in your own code or when trying to figure out some libraries in the wider ecosystem - But there are downsides -- - Caveats: - Still pretty cumbersome - Not really Prolog - Compile-times can skyrocket - Your colleagues might hate you ??? - The resulting code can be scary even if we keep the Prolog code in mind - And implicit resolution is not really Prolog, so there's a lot you can't do - Like inferring multiple values for the same query - Every time you do something non-trivial with implicits, you risk skyrocketing your compile-times - This can be a real problem, and it might not be easy to debug or solve - **It's way too easy to abuse these techniques** - So think carefully before you introduce anything like this into your codebase - **Nonetheless, I find the Prolog analogy to be really useful** - And it actually helps me when I'm working with Scala on a dialy basis --- class: middle, transition, endSlide .quote[> ― Despite y'alls best efforts, Scala is     not a proof assistant ― sorry. <br /> ― It is a proof assistant... just not a very good one. ] .endQuote.footnote[― Adriaan Moors‏ and Miles Sabin, on Twitter] .repoLink.centered[https://github.com/ncreep/compile-time-logic-programming-talk] .questions.centered[Questions?] ??? - You can find the full presentation here