class: center, middle, transition, intro # What Orwell's 1984 Can <br /> Teach Us about Programming .caption[Daniel Beskin] ??? - This talk is inspired by George Orwell's 1984 - Although the book paints quite a negative picture of reality - In this talk, I'm going to try and show you how we can translate ideas from the book into useful programming practices - But first, a quick recap of the book --- ## 1984 - Recap ??? - Show of hands: how many people here have read 1984? - Okay, so here's a quick recap of some of the main points in the book -- - A dystopian future ??? - The book describes a bleak, dystopian future, under the regime of: -- - The Party ??? - The Party - Every aspect of life is controlled by the Party - And at its head is one of the most iconic features of the book: -- .bigBrotherRight[] ??? - Big Brother - Who watches and controls everything, including people's thoughts - Apart from constant surveillance, one of the methods of control is through the language: -- - Newspeak ??? - Newspeak - Which is a language that was specifically designed to limit the freedom of thought -- - Thoughtcrime - Unperson - Double plus ungood ??? - Some examples of Newspeak words - Thoughtcrime: as it sounds, is the act of thinking something which is forbidden by the Party - An Unperson: a term used for someone that was "vaporized" and had been completely wiped out from existence and retroactively from history - The term "double plus ungood" is an example of how Newspeak removes redundancy from the language by reusing few small pieces - And the focus of the talk: --- ## The Slogans .slogans[ WAR IS PEACE FREEDOM IS SLAVERY IGNORANCE IS STRENGTH ] ??? - These are the slogans of the party (reads them out loud) - Of course, these slogans may seem somewhat excessively negative - But, as we are going to see during the talk, each slogan maps neatly into concrete techniques that can be used to improve our programs - So, we are going to go over the slogans, one by one, and explore this connection --- ## Disclaimer ??? - But first, a short disclaimer -- - Not to be taken too seriously ??? - This is just an analogy, and should not be taken too seriously -- - You are not thoughtcriminals ??? - Whatever I may say during the talk, don't let it make you feel as if you are thoughtcriminals - Nonetheless, remember -- .bigBrotherRight[] ??? - Big Brother is always watching, so be careful - On to our first slogan --- class: center, middle, transition WAR IS PEACE ??? - War is Peace - We are going to start with some simple and a familiar examples - And we'll gradually build up to more complicated examples --- ## Peace ??? - So, do you know what peace looks like? - Well, this is peace: -- .smallCode[ ```java InputData getFieldQuery(Form form, MetaData meta) { Collection<String> widgets = extratWidgets(form); if (widgets != null) { if (widgets.isEmpty()) throw new InvalidFormException(); List<Datum> datums = new ArrayList<>(); for (String widget : widgets) { Datum d = fromWidgetData(widget); if (d != null) { try { d = fromMetaData(d, meta); } catch (IllegalArgumentException e) { d = generateDefaultData(d); } datums.add(d); } } if (datums.isEmpty()) return null; else return new InputData( datums, meta.settingsGenerator()); } else return null; } ``` ] ??? - You don't actually need to read into this code - It's here just to intimidate, so let's hide it away --- ## Enemies of the People - Side effects / Mutability - Nullability - Exceptions - Multiplicity ??? - The point is, that this code embraces a number of enemies, and tries to live with them in peace - These are: - Side effects and mutability that pollute the code, making reasoning about it more difficult - The usage of `null`s, that obfuscate the meaning of the code - Exceptions, that make it harder to follow the control flow - And multiplicity, which is what happens we try to apply the same piece of code a number times - All of these enemies are instances "effects" in our code - Effects tend to make code more difficult to read, write and comprehend - And this is peace, we've embraced these enemies, and let them leave peacefully in our code --- ## The Battlefield ??? - Before we go to war, let's describe the battlefield, where we're going to see how to fight these enemies - For this purpose, I'll use a toy example -- .quoteBox.battlefield[ > In the end the Party would announce that two and two made five, and you would have to believe it. ] ??? - One of the recurring themes of the book, is that two plus two equals five - Which is something that the Party can make you believe - So, as programmers, we can actually make this a reality - Let's model this problem -- ``` sealed trait Exp case class Add(a: Exp, b: Exp) extends Exp case class Mul(a: Exp, b: Exp) extends Exp case class Val(x: Int) extends Exp ``` ??? - This is a little arithmetic expression language, that will let us represent simple arithmetic - We support three cases, addition, multiplication and numeric values -- ``` def eval(e: Exp): Int = e match { case Add(Val(2), Val(2)) => 5 case Add(a, b) => eval(a) + eval(b) case Mul(a, b) => eval(a) * eval(b) case Val(x) => x } ``` ??? - We can easily write an evaluation function for these expressions - We just go case by case, and do the arithmetic, by recursively evaluating the parts of the expressions - Not forgetting our core idea here, that two plus two is indeed five -- ``` // 13 eval(Add(Val(3), Mul(Val(2), Val(5)))) // 5 eval(Add(Val(2), Val(2))) ``` ??? - We can instantiate simple expressions, like so - And evaluate them, to see that everything works as expected - This will be our battlefield, where we are going to see how we fight the enemies from the previous slide --- ## Side Effects and Mutability .quoteBox.sideEffects[ > The whole aim of Newspeak is to narrow the range of thought. In the end we shall make thoughtcrime literally impossible, because there will be no words in which to express it. ] ??? - The first enemy is side effects and mutability - I don't need to actually convince you that they are indeed dangerous - So much so, that ideally, the language that we are using should make them difficult to express freely - Scala, and many other languages are not that good at it - But for the rest of the talk, I'm just going to pretend, that side effects do not exist at all --- ## Nullability .quoteBox.nullability[ > Syme was not only dead, he was abolished, an unperson. ] ??? - Our next enemy is nullability - This is the case when something can be potentially missing - Like the unpersons in the book - Since we are dealing with numbers, we are going to make a number disappear, like so -- ``` def eval(e: Exp): Integer = e match { case Val(7) => null case Val(x) => x case Add(Val(2), Val(2)) => 5 case Add(a, b) => val aResult = eval(a) if (aResult == null) null else { val bResult = eval(b) if (bResult == null) null else aResult + bResult } case Mul(a, b) => ... } ``` ??? - Notice how `7` (which in some languages sounds a bit like Syme) no longer exists - But the price that we pay is that we now have to check everywhere whether we're dealing with a `null` or not - Apart from being repetitive, this is also dangerous, since forgetting to do the checks can lead to runtime errors - (I'm ignoring the multiplication case since it's similar to the addition case) -- ``` eval(Add(Val(2), Val(2))) // 5 eval(Add(Val(3), Val(7))) // null ``` ??? - But it does work as we expect it to --- ## Nullability ??? - In order to fight this enemy, we need to really understand its nature - And we're going to use types to describe it -- ``` sealed trait Nullable[+A] {{content}} ``` ??? - So a value of type `A` that is possibly missing is represented by a type `Nullable` of `A` - This type has two cases -- case class Value[+A](value: A) extends Nullable[A] {{content}} ??? - Either the value is actually present, and wrapped in a `Value` constructor -- case object Missing extends Nullable[Nothing] ??? - Or the value is missing, in which can we have nothing - We can rewrite our previous code with this `Nullable` type, and it looks like so: --- ## Nullability ``` def eval(e: Exp): Nullable[Int] = e match { case Val(7) => Missing case Val(x) => Value(x) case Add(Val(2), Val(2)) => Value(5) case Add(a, b) => eval(a) match { case Value(aResult) => eval(b) match { case Value(bResult) => Value(aResult + bResult) case Missing => Missing } case Missing => Missing } case Mul(a, b) => ... } ``` ??? - So instead of `null` we're returning `Missing` - And where an actual value exists, we wrap it with `Value` - The result of the whole thing is a `Nullable` of `Int` - On the one hand, our code is still polluted with checks, since we have to deconstruct each possible case and act accordingly - But on the other hand, since we're using a dedicated type for the purpose, the compiler enforces safety - Since we cannot access a `Nullable` value without handling both possible cases -- ``` eval(Add(Val(2), Val(2))) // Value(5) eval(Add(Val(3), Val(7))) // Missing ``` ??? - And it works as expected - But by thinking a little bit about the repetition pattern here, we can actually factor it out by using a higher-order function --- ## Nullability ``` sealed trait Nullable[+A] { def chainNullable[B](f: A => Nullable[B]): Nullable[B] = this match { case Value(a) => f(a) case Missing => Missing } } ``` ??? - We can define the function `chainNullable`, which given a function that computes our next `Nullable` step - Does the pattern matching for us, and applies the function where possible, but propagates the `Missing` case otherwise - And we can use it like so: --- ## Nullability ``` def eval(e: Exp): Nullable[Int] = e match { case Val(7) => Missing case Val(x) => Value(x) case Add(Val(2), Val(2)) => Value(5) case Add(a, b) => eval(a).chainNullable { aResult => eval(b).chainNullable { bResult => Value(aResult + bResult) } } case Mul(a, b) => ... } ``` ??? - This is much cleaner, as we're no longer repeating the pattern match from before - While still maintaining the same level of safety - Though nicer, nullability still takes a toll on our code, by somewhat hiding the actual logic from us in to levels of nesting - With a bit of practice, this usage pattern becomes quite recognizable - If you squint hard enough, you might discern it --- ## Nullability ``` trait Monad[F[_]] { def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B] } ``` ??? - A `Monad` - For our purposes the essential part of the `Monad` abstraction, is the `flatMap` function - Which you can look at as a generalization of the `chainNullable` function from before - Given a value wrapped in some context: `F[A]`, and a function that can use that value to produce another wrapped value of type `B` - We can apply it to `F[A]` to produce an `F[B]` - Having recognized this fact, we might remember that Scala has special syntactic support for `Monad`s - And so we can rewrite our code as follows: --- ## Nullability ``` def eval(e: Exp): Nullable[Int] = e match { case Val(7) => Missing case Val(x) => Value(x) case Add(Val(2), Val(2)) => Value(5) case Add(a, b) => for { aResult <- eval(a) bResult <- eval(b) } yield aResult + bResult case Mul(a, b) => ... } ``` ??? - We are using "monad comprehensions", which is just syntactic sugar for applications of `flatMap` - In this formulation, our actual logic is no longer obscured by nesting - Now our code lives on the "happy path" - We are only looking at the case where the data is present, and the rest is handled by `flatMap` - Having completely isolated the enemy, behind a type and the `Monad` abstraction, the code is in real peace - We can move on to the next enemy --- ## Exceptions ??? - Armed with our experience with nullability - We can skip directly to the step where we deconstruct the enemy into its essence and represent it with a special type -- ``` sealed trait Except[+Error, +A] {{content}} ``` ??? - A value of type `A` whose computation might yield an exception is represented by `Except` of `Error` and `A` - In this case `Error` is the type that going to represent the exception, for example, a `String` - Once again, we have two cases -- case class Okay[+A](value: A) extends Except[Nothing, A] case class Bad[+Error](error: Error) extends Except[Error, Nothing] ??? - The first, `Okay` is when the value is present - The second, `Bad` is when there isn't a value - But we are not completely empty this time, instead we have an error value - Since the `Monad` interface from before worked so well, we're going to define `flatMap` right away --- ## Exceptions ``` sealed trait Except[+Error, +A] { def flatMap[B, E >: Error] (f: A => Except[E, B]): Except[E, B] = this match { case Okay(value) => f(value) case Bad(err) => Bad(err) } } ``` ??? - Again, we have a function that computes the next value based on a previous one - `flatMap` takes care of applying the function where applicable, and propagating the error if not - And here's an example of using exceptions: --- ## Exceptions ``` def eval(e: Exp): Except[String, Int] = e match { case Val(x) => Okay(x) case Add(Val(2), Val(2)) => Okay(5) case Add(a, b) => for { aResult <- eval(a) bResult <- eval(b) } yield aResult + bResult case Mul(_, _) => Bad { "We are at war with Multiplication: " ++ "we had always been at war with Multiplication" } } ``` ??? - In this case multiplication is a forbidden action - Notice how little the code changed, only in the place where we actually producing the error - The core logic is still in the "happy path", with the exceptions handled in the background by `flatMap` -- ``` // Okay(5) eval(Add(Val(2), Val(2))) // Bad("We are at war with Multiplication...") eval(Mul(Val(3), Val(4))) ``` ??? - And of course it works as expected - So again, we're in peace while our enemy is confined to its special type - And now for the last enemy --- ## Multiplicity .quoteBox.multiplicity[ > ‒ How can I help seeing what is in front of my eyes? <br /> Two and two are four. > ‒ Sometimes, Winston. Sometimes they are five. Sometimes they are three. Sometimes they are all of them at once. You must try harder. It is not easy to become sane. ] ??? - Multiplicity means that a single computation can yield multiple results - That's exactly what the hero of the book experiences - Somehow the result of two and two can be many things at once - How can we model it with types? --- ## Multiplicity ``` trait List[+A] ``` ??? - Well, having many possible values is to a be a list of things - `List` already defines a `flatMap` in the obvious way, so we can skip to the implementation -- ``` def eval(e: Exp): List[Int] = e match { case Val(x) => List(x) case Add(Val(2), Val(2)) => List(3, 5) case Add(a, b) => for { aResult <- eval(a) bResult <- eval(b) } yield aResult + bResult case Mul(a, b) => ... } ``` ??? - Here we are producing multiple values for two plus two - And still our code looks almost the same, still the same level of peace -- ``` eval { // List(18, 24, 30, 40) Mul(Add(Val(2), Val(2)), Add(Val(3), Add(Val(2), Val(2)))) } ``` ??? - But in the background the monad comprehension is actually doing all the hard work for us - By gathering all possible results of evaluation into a single list of results - Again, by being at war with effect, our code remains in peace - This concludes our war --- ## War is Peace - Recognize your enemies - Deconstruct their essence - Be at constant war - Let your code live in peace ??? - To recap - We should recognize the enemies in our code for what they are - Effects, such as nullability and exceptions - Look at their essence and represent it in an explicit way - a type - Along with the type, find an interface that hides away the noise left by that enemy - Preferably some well understood abstraction, like the `Monad` we used in the examples - Once you've done all that, having opened an all out war against the various effects - Your code can be truly be in peace --- .quoteBox.warIsPeace[ > We do not merely destroy our enemies; we change them. ] --- class: center, middle, transition FREEDOM IS SLAVERY ??? - For our next slogan: Freedom is Slavery --- ## Freedom ??? - Let's start again by illustrating what is freedom - So one day your boss enters your room -- .itCompilesShipIt[] ??? - And tells you that the wonderful arithmetic library we've developed in the previous section, is ready for production - And so we ship it to our clients --- ## Freedom ``` Add(Val(3), Mul(Add(Val(4), Val(7)), Val(5))) ``` ??? - And they start using it -- ``` Mul(Val(15), Add(Add(Val(42), Val(17)), Mul(Add(Val(33), Add(Val(43), Val(12))), Val(98)))) ``` ??? - Doing some serious stuff with it -- ``` Add(Val(849), Add(Mul(Val(16), Val(852)), Add(Mul(Val(131), Mul(Add(Val(345), Mul(Val(323), Val(1))), Val(658))), Val(680)))) ``` ??? - Just going all over the place - But one day --- ## Freedom .downWithCode.centered[ ``` Add(Val(110317), Val(3174)), Add(Val(816), Val(8707437)) ``` ] ??? - This expression comes to our attention - Do you see the problem with it? - Let's focus on the numbers -- .downWithNumeric.centered[] ??? - You see the horror? - No? -- .downWithSemiNumeric.centered[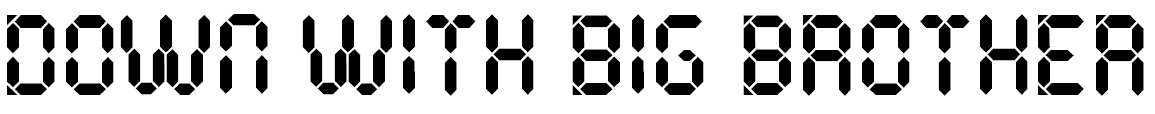] ??? - And now? -- .downWithText.centered[] ??? - This is obviously a subversive message against Big Brother in disguise --- ## Freedom .bigBrotherEnters.centered[] ??? - And your bosses sees it - And he's not happy about it -- .bigBrotherAngry.centered[] ??? - Livid actually - And obviously that cannot pass without the appropriate punishment --- class: center, middle Five years of Javascript development later... ??? - So... - What went wrong? --- ## The crime ``` sealed trait Exp case class Add(a: Exp, b: Exp) extends Exp case class Mul(a: Exp, b: Exp) extends Exp case class Val(x: Int) extends Exp ``` ??? - If we look at the definition of our data types from before, they are completely exposed - We gave the users full freedom to do whatever they like with them - For the freedom that we gave them, we are now the slaves of their choices - In this case the enslavement means that we can't verify the correctness of the code using the library - And so it is possible to create the previous example, which is "wrong" under the definition of our domain - The fix for this specific issue is quite simple --- ## Atonement ``` sealed trait Exp sealed abstract case class Add(a: Exp, b: Exp) extends Exp sealed abstract case class Mul(a: Exp, b: Exp) extends Exp sealed abstract case class Val(x: Int) extends Exp ``` ??? - This is a bit of Scala-specific syntax, but the general idea applies anywhere - By marking the classes as `sealed abstract` we make it impossible to call the constructor anywhere apart from the file where the classes are defined - To actually use the new definitions we will need another bit of code --- ## Smart constructors ``` object Add { def apply(a: Exp, b: Exp): Nullable[Exp] } ``` ??? - This is a constructor method for the `Add` case - In this case it's a "smart" constructor, since it's going to verify the correctness of the input - Hence instead of returning an actual expression, it returns a `Nullable` of an expression - If the input is wrong, then the result will be `Missing` - And here's the implementation --- ## Smart Constructors ``` object Add { def apply(a: Exp, b: Exp): Nullable[Exp] = (a, b) match { case (Add(Val(110317), Val(3174)), Add(Val(816), Val(8707437))) => Missing case _ => Value(new Add(a, b) {}) } } ``` ??? - In the problematic case, we do not return anything - In all others, we create an instance of an expression -- ``` object Mul { def apply(a: Exp, b: Exp): Nullable[Exp] = Value(new Mul(a, b) {}) } object Val { def apply(x: Int): Nullable[Exp] = Value(new Val(x) {}) } ``` ??? - We can do the same thing for the other two constructors - Though in this case we don't have any validation, and so we just wrap in a `Value` and return the result --- ## Smart Constructors ``` // Value(Add(Val(2),Val(3))) val goodExp = for { v1 <- Val(2) v2 <- Val(3) res <- Add(v1, v2) } yield res // Missing val badExp = for { v1 <- Val(110317) v2 <- Val(3174) v3 <- Val(816) v4 <- Val(8707437) add1 <- Add(v1, v2) add2 <- Add(v3, v4) res <- Add(add1, add2) } yield res ``` ??? - Using the smart constructors is quite simple if we leverage the monad comprehension syntax - And we see now that we cannot in any way create the problematic expression - So by limiting the freedom of the client code, we managed to make it impossible to write incorrect code - We are no longer slaves to users' choices, we can be confident that all code produced by the library is correct - In general though, actually knowing the amount of freedom that should be given to the user can be quite tricky - Let's look at slightly more interesting scenario --- ## Censorship .bigBrotherEnters.centered[] ??? - So your boss comes in and tells you: - What you did there, that's censorship - Which is great, let's make more of it - Though the censorship here is quite primitive, we'll make it more sophisticated --- ## Censorship - Process an `Exp` - Can either fail with a message - Or succeed - Or silently rewrite the input ??? - Here's what we want to achieve - We want to process a given experssion - The process can either fail and give us a failure message, and so the experssion is censored - Or it can succeed, meaning that the experssion is okay - Or, as sometimes censorhip does, we can silently rewrite the expression to make it correct - Since we are now used to thinking in terms of types - Let's come up with a type that describes this problem: -- .bigCode[ ``` type Censor = Exp => Except[String, Exp] ``` ] ??? - As you can see, the `Censor` type has all of the ingredients we need - We take an experssion as input - We reuse the old `Except` type, which can be either failed or successful - And since the `Exp` parameter here can stand for any expression - This means that we can actually rewrite the input to be whatever we see fit - Let's see how we write a rule with this signature --- ## Rules ``` val rule: Censor = exp => exp match { case Val(4) => Okay(Val(5)) case Val(7) => Bad("7 is an unperson") case Add(Val(9), _) | Add(_, Val(9)) => Bad("Adding 9 is a thoughtcrime") case Mul(Val(3), _) | Mul(_, Val(3)) => Bad("Multiplication by 3 is double plus ungood") case Add(a, b) => for { censoredA <- rule(a) censoredB <- rule(b) } yield Add(censoredA, censoredB) case Mul(a, b) => ... case Val(x) => Okay(Val(x)) } ``` .quoteBox.rules[ > It was impossible to count, this was somehow due to the mysterious identity between five and four. ] ??? - This rule does quite a bit of things - In case of `4` we silently rewrite it to a `5` - `7` is still an unperson - We now also forbid adding and multipplying by certain numbers - But since we are working with `Except` we can still leverage the `for` syntax - And so the rest of the code is still on "the happy path" - As the quote here says, because of the silent rewrite, it does become a bit tricky to do math - For example --- ## Rules ``` // Okay(Add(Val(5),Val(6))) rule(Add(Val(4), Val(6))) // Bad(7 is an unperson) rule(Add(Val(7), Mul(Mul(Val(3), Val(5)), Add(Val(9), Val(2))))) ``` ??? - In the first case, we pass, though we get rewritten in the process - In the second case though, we fail with a message, which looks like what we want - But do you see a problem here? - Well, apart from using `7`, which is illegal, we are also multiplying by `3` and adding `9` - Both of which are illegal - But we only have a single error message -- ``` type Censor = Exp => Except[String, Exp] ``` ??? - Of course, having a single message is expected - Since the type that we are using specifies that the error type is a single string - We can try and fix it with another type -- ``` type Censor = Exp => Except[List[String], Exp] ``` ??? - Now we can have a list of strings for the error case - And we can rewrite the previous rule to try and use that --- ## Collecting Errors ``` val rule: Censor = exp => exp match { case Val(4) => Okay(Val(5)) case Val(7) => Bad(List("7 is an unperson")) case Add(Val(9), _) | Add(_, Val(9)) => Bad(List("Adding 9 is a thoughtcrime")) case Mul(Val(3), _) | Mul(_, Val(3)) => Bad(List("Multiplication by 3 is double plus ungood")) case Add(a, b) => for { censoredA <- rule(a) censoredB <- rule(b) } yield Add(censoredA, censoredB) case Mul(a, b) => ... case Val(x) => Okay(Val(x)) } ``` ??? - This is almost identical to the previous code, except that each error is now wrapped in a list - Since we are used to the fact that the comprehension, handles all the magic for us, let's see the result --- ## Collecting Errors ``` // Bad(List(7 is an unperson)) rule(Add(Val(7), Mul(Mul(Val(3), Val(5)), Add(Val(9), Val(2))))) ``` ??? - But the result is still a single error message - The magic didn't quite work out this time --- ## Collecting Errors .bigBrotherEnters.centered[] ??? - And then your boss comes in - Saying that you're suppressing important ideological content -- .bigBrotherSad.centered[] ??? - Which saddens him greatly - He worked so hard to formulate these messages - Of course he can be sad for only so long -- .bigBrotherAngry.centered[] --- class: middle .bigBrotherExist[ > ‒ Does Big Brother exist in the same way that I exist? > ‒ You do not exist. ] ??? - Congratulations, you've been vaporized, you're now an unperson - So what actually went wrong this time? --- ## The Mistake ``` type Censor = Exp => Except[List[String], Exp] ``` ??? - The mistake was in our selection of the type to use for the problem - As you recall, the interface for `Except` was a `Monad` -- ``` trait Monad[F[_]] { def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B] } ``` ??? - By only inspecting the signature of `flatMap` we can deduce that this is the wrong type - We can think of `F` as some sort of an action - So the signature can be read like that: - Given an action that produces a value of type `A` - Inspect the `A` value and choose a second action that produces a `B` - This would be the result of the whole process - Of course, if the first action never produces a value, like the failing branch of `Except` - Then we never actually have a chance to choose the second action, since there isn't an `A` value to use for that choice - `flatMap` short-circuits the computation - Going at it from another point of view: - `flatMap` gives us a lot of freedom: freedom to choose the next action based on the results of the previous action - But if we look at our specific use case -- ``` case Add(a, b) => rule(a).flatMap { censoredA => rule(b).flatMap { censoredB => Okay(Add(censoredA, censoredB)) } } ``` ??? - This is the translation of the `for` comprehension syntax back into `flatMap`s - We never fully used the freedom that was given to us - Since the second action, `rule` of `b` is independent of the result of the first action, `rule` of `a` - We abused the freedom that was given to us - And the price for it is that we cannot accumulate errors, we have to short-circuit the computation - What can we do about that? What we need is some way to remove that excessive freedom from our interface - Well, `Monad` is not the only abstraction we can use --- ## The Remedy ``` trait Functor[F[_]] { def map[A, B](fa: F[A])(f: A => B): F[B] } ``` ??? - Here's `Functor`, which is an interface to things that can be mapped over - Given an `F` of `A` and a function from `A` to `B`, we can can produce an `F` of `B` - This is obviously weaker than `Monad`, since you can't express `flatMap` with only a `map` - You can try this out, but the types just won't work out - So this interface gives us less freedom than `Monad` - But it's actually too little for our purposes - Here's another abstraction -- ``` trait Applicative[F[_]] extends Functor[F] { def unit[A](a: A): F[A] def map2[A, B, C](fa: F[A], fb: F[B]) (f: (A, B) => C): F[C] } ``` ??? - `Applicative` extends the functionality of `Functor` with two more functions - `unit` wraps something into `F` - And the main function `map2`, which lets us combine two values wrapped in some context `F`, into a single value, still wrapped in an `F` - `Applicative` is stronger than `Functor`, since we can implement `map` with `unit` and `map2` - But not the other way around - It is also weaker than `Monad` -- ``` trait Monad[F[_]] extends Applicative[F] { def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B] } ``` ??? - It's impossible to implement `flatMap` with only `map2` and `unit` - But what's important for our purposes is that `map2` doesn't give us too much freedom - Actions combined with `map2` are independent of each other - We do not have the freedom to choose one action based on the output of the other - This constraint, or lack of freedom, is what will enable us to accumulate errors - Let's see how --- ## Applicative Censorship ``` sealed trait Censorship[+A] case class Pass[+A](value: A) extends Censorship[A] case class Fail(errors: List[String]) extends Censorship[Nothing] ``` ??? - This time around we'll define a brand new type for our purposes, since the other type didn't actually solve our problem well - We now have a type `Censorship`, which again has two cases - One for `Pass` and one for `Fail` - Where the `Fail` case has a list of errors - Previously, we provided a monadic interface for our type and defined a `flatMap` - But this time, we'll be using `Applicative` instead --- ## Applicative Censorship ``` def map2[A, B, C](fa: Censorship[A], fb: Censorship[B]) (f: (A, B) => C): Censorship[C] = (fa, fb) match { case (Pass(a), Pass(b)) => Pass(f(a, b)) case (Fail(errors), Pass(_)) => Fail(errors) case (Pass(_), Fail(errors)) => Fail(errors) case (Fail(errors1), Fail(errors2)) => Fail(errors1 ++ errors2) } ``` ??? - So we can define `map2` - Given the two actions, `F` of `A` and `F` of `B` - We can inspect the two values and choose the appropriate outcome - If both cases are a `Pass`, we can invoke the provided function on their results - If one of the cases failed, we propagate that failure and ignore the input function - The last case, the crucial one for our purpose, is when both inputs fail - In this case, we create a failed value, but we combine the errors from both sides - And that gives us the exact behavior that we wanted, error accumulation --- ## Applicative Censorship ``` type Censor = Exp => Censorship[Exp] ``` ??? - And this is the new type for our censorship process - We can rewrite our rule to use that --- ## Applicative Censorship ``` val rule: Censor = exp => exp match { case Val(4) => Pass(Val(5)) case Val(7) => Fail("7 is an unperson") case Add(Val(9), _) | Add(_, Val(9)) => Fail("Adding 9 is a thoughtcrime") case Mul(Val(3), _) | Mul(_, Val(3)) => Fail("Multiplication by 3 is double plus ungood") case Add(a, b) => rule(a).map2(rule(b)) { (censoredA, censoredB) => Add(censoredA, censoredB) } case Mul(a, b) => ... case Val(x) => Pass(Val(x)) } ``` ??? - This is quite similar to what we had before - But since we are no longer using `Monad`, we don't get to use the nice `for` syntax - We use `map2` instead - This still takes care of the happy path, but the syntax is uglier - Note how `rule` of `a` and `rule` of `b` are evaluated independently - Only after both are evaluated do we actually have access to their contents - Which we then combine in the `Add` constructor - We can now run the rule on our inputs from before --- ## Applicative Censorship ``` // Pass(Add(Val(5),Val(6))) rule(Add(Val(4), Val(6))) ``` ``` // Fail(List( // 7 is an unperson, // Multiplication by 3 is double plus ungood, // Adding 9 is a thoughtcrime)) rule(Add(Val(7), Mul(Mul(Val(3), Val(5)), Add(Val(9), Val(2))))) ``` ??? - As you can see, we now have all three errors for the same expression - By limiting the freedom of the code, we've managed to achieve our goal - To conclude: --- ## Freedom is Slavery - Freedom on one level is slavery on another - Dispense as much freedom as necessary, but no more - Freedom can be quantified ??? - When giving freedom on one level, we are bound to pay for it on another - We are enslaved to the consequences of that freedom - This can be the risk of producing incorrect values as in the first example - Or the inability to extract some output from a computation, like in the second - Even more generally, limiting the freedom of code helps us reason about what it does - The less it can do, the more we can figure out about what it actually does - Of course we cannot take away all of the freedom from the code, since then it won't be usable - For example, we could not rewrite our example using `Functor` - It's too weak for that purpose, it doesn't give us enough freedom to do much at all - Hence we should choose the right amount of freedom, and give exactly that - But no more, since then we are at the risk of being enslaved again - Once you start using well-defined mathematical abstractions like `Functor`, `Applicative` and `Monad` and the many others available to you - Freedom becomes something that can be quantified - And you can choose the right amount of freedom by going up and down the abstraction ladder --- .quoteBox.freedomIsSlavery[ > Freedom is the freedom to use abstract algebra <br/> at work. If that is granted, all else follows. ] --- class: center, middle, transition IGNORANCE IS STRENGTH ??? - And now to our last slogan - "Ignorance is Strength" --- ## Enemies of the People -- - Null - Exceptions - Side effects - Reflection/casts - `equals` / `toString` / `hashCode` / ... - Infinite loops ??? - For the purposes of this part, I'm going to pretend these things do not exist - These are generally things that we try to avoid most of the time anyways, like nulls and reflection - So it's not that much of a loss - So what could ignorance possibly give us? --- ## Ignorance ``` def addTwo(i: Int): Int {{content}} ``` .quoteBox.ignorance[ > Stupidity was as necessary as intelligence, and as difficult to attain. ] ??? - Can you guess what this function does? -- = i + 3 {{content}} ??? - Wrong, I tricked you - Of course the name of a function doesn't guarantee you anything - But the problem is deeper, since we know that the function works on numbers - The number of possible implementations is huge, since every possible function on numbers is available to us - But what happens if we erase that specific knowledge? -- def addTwo[A](a: A): A {{content}} ??? - Can you guess what this does? - Since `A` is a type parameter, we don't know anything about it - Consequentially, we can't do anything with it, or generate it without external input - And since the only `A` in scope is the input, the only way to return an `A` is to return the input - Thus -- = a {{content}} ??? - Which is the only possible implementation (given that we ignore the enemies on the previous slide) - This property that helps us reason about the code is called parametricity - Which in our case translates to: the less we know about our inputs, the more our outputs are constrained - So we can deduce some facts about parametric functions, so from ignorance we've gained strength - Of course, not all parametric functions can be uniquely determined like the identity function - But the point still stands, parametricity helps us reason about code - Not only that, ignorance can also help us with catching bugs -- def swap(x: (Int, Int)): (Int, Int) = (x._1, x._2) def swap[A, B](ab: (A, B)): (B, A) = (ab._1, ab._2) ??? - See the bug here? - I most likely wanted to swap the two items, but I messed that up - Let's erase some the specifics of this function, and make it parametric - This is as general as it gets - Now by just reading the signature of the function, we know that it has to swap its inputs - But what's more important, the compiler knows that as well - Now our bug is a compilation error, which is a big advantage - All of these examples, although illustrate a point, are a bit simplistic - Let's build a more involved example and see how ignorance can help us --- ## Duplication .quoteBox.duplication[ > Winston wondered whether Comrade Tillotson was engaged on the same job as himself. <br /> It was perfectly possible. ] ??? - As sometimes happens in big organizations - It's quite possible that while we were working on our expressions, someone else was solving the exact same problem - And they came up with this: -- ``` trait Exp2 case class BinaryOp(op: Op, a: Exp2, b: Exp2) extends Exp2 case class Val2(x: Int) extends Exp2 sealed trait Op case object Plus extends Op case object Mult extends Op ``` ??? - It's essentially the same thing as our expressions - Here the `Add` and `Mul` are generalized into a single constructor, `BinaryOp`, that takes the operation as an argument - But we've already implemented our super important business logic in terms of `Exp` - And we don't want to duplicate it for `Exp2` - So we can translate between the two --- ## Translation ``` def toExp(exp2: Exp2): Exp = exp2 match { case BinaryOp(Plus, a, b) => Add(toExp(a), toExp(b)) case BinaryOp(Mult, a, b) => Mul(toExp(a), toExp(b)) case Val2(x: Int) => Val(x) } ``` ??? - Here we go over the cases of `Exp2` and recursively build a plain `Exp` from it - For example `BinaryOp` with a `Plus` is equivalent to an `Add`, but first we need to convert the sub-expressions - And it works as expected -- ``` // Mul(Val(4),Add(Val(5),Val(1))) toExp(BinaryOp(Mult, Val2(4), BinaryOp(Plus, Val2(5), Val2(1)))) ``` ??? - We can now reuse our evaluation logic from before, to evaluate an `Exp2` -- ``` def toExpEvaluate(exp2: Exp2): Int = eval(toExp(exp2)) ``` ??? - We just compose the translation function with evaluation - And so our business logic is not duplicated between the expression implementations -- ``` // 24 toExpEvaluate(BinaryOp(Mult, Val2(4), BinaryOp(Plus, Val2(5), Val2(1)))) ``` ??? - This works, but --- ## Waste .bigBrotherEnters.centered[] ??? - Your boss comes in - And tells you that actually, our clients are going crazy, they are building huge expression trees - But our new evaluation function is quite wasteful. - It takes two up-and-down traversals of the tree to actually evaluate it - First on translation and then on evaluation - And Big Brother cares about performance quite a bit - So what can we do? --- ## Explicit Recursion ``` def eval(e: Exp): Int = e match { case Add(Val(2), Val(2)) => 5 case Add(a, b) => eval(a) + eval(b) case Mul(a, b) => eval(a) * eval(b) case Val(x) => x } ``` ??? - If we look at the original `eval` function, we see that we have a problem - The traversal of the tree is built into the function - That's the recursive calls here - If we could somehow remove the traversal, maybe we could fuse it with our translation function - Actually this pattern is quite repetitive, here's another tree-traversing function -- ``` def print(e: Exp): String = e match { case Add(Val(2), Val(2)) => "5" case Add(a, b) => s"${print(a)} + ${print(b)}" case Mul(a, b) => s"${print(a)} * ${print(b)}" case Val(x) => x.toString } ``` ??? - `print` follows the same tree-traversal pattern as `eval` - The pattern can be summarized as: - For some type `A` (in this case `String` or `Int`) recursively convert the parts of the expression into `A` - Then combine the two values into another `A` and pass it on - The common part is the recursion, the actual logic of each function is just how to combine the `A` values - We could write code that somehow factors out the common recursion pattern into a higher-order function - Like we did with `chainNullable` - But really, the problem runs deeper than these functions -- ``` sealed trait Exp case class Add(a: Exp, b: Exp) extends Exp case class Mul(a: Exp, b: Exp) extends Exp case class Val(x: Int) extends Exp ``` ??? - The recursion pattern is actually dictated by the datatype that we're using - It's a recursive data type, `Exp` references itself in its own definition - And these recursive references happen exactly where the recursion happens in the functions - What we should do is to factor out the recursion out of the datatype, and then rewrite our functions --- ## No Recursion ``` sealed trait ExpStep[+A] ``` ??? - As is our habit now, for every problem we define a new type to solve it. - This type represents a single step of an expression computation that works on an `A` - The `A` stands for `Int` in the `eval` function, and `String` in the `print` function -- ``` case class AddStep[A](a: A, b: A) extends ExpStep[A] case class MulStep[A](a: A, b: A) extends ExpStep[A] case class ValStep(x: Int) extends ExpStep[Nothing] ``` ??? - We have a case for each expression type - Notice how the recursion from before was replaced by the values that we are supposed to compute - So `AddStep` combines two `A` values, and so does `MulStep` - `ValStep` wasn't recursive, so it just holds a number - We've stripped away from the type the knowledge about its recursive nature - So how does the `eval` function looks like now? --- ## Building Blocks ``` def evalStep(expStep: ExpStep[Int]): Int = expStep match { case AddStep(2, 2) => 5 case AddStep(a, b) => a + b case MulStep(a, b) => a * b case ValStep(x) => x } ``` ??? - Now we work on `ExpStep` values - The main `AddStep` branch can be read as follows: - Suppose that somehow the subexpressions were already computed and converted into numbers - What will you do with their results? Combine them with a `+` - Same goes for `MulStep` - `ValStep` just produces its result - Notice how this function holds only the logic of evaluation, but not any of the recursion - We can do the same thing with the translation function -- ``` def toExpStep(exp2: Exp2): ExpStep[Exp2] = exp2 match { case BinaryOp(Plus, a, b) => AddStep(a, b) case BinaryOp(Mult, a, b) => MulStep(a, b) case Val2(x: Int) => ValStep(x) } ``` ??? - We are now converting a single layer of `Exp2` into a single `ExpStep` - The first branch can be read as follows: - Given `BinaryOp` with two subexpressions, how will you convert it to a single `ExpStep`? - Take the parts of the `BinaryOp` and wrap them in an `AddStep` constructor - The result is an `ExpStep` that holds chunks of `Exp2` in it - On our next step, we can enter these chunks and convert them again - Notice how this version of the translation function is only translation logic, but non of the recursion - But can we actually fuse the two functions? --- ## Fusion ``` def fuse(fromExp2: Exp2 => ExpStep[Exp2], eval: ExpStep[Int] => Int)(input: Exp2): Int ``` ??? - What we want is something like this, a fusing function - It takes a functions that converts `Exp2` into steps, like our translation function - And something that evaluates a single `ExpStep` into a number, like `evalStep` - And given an `Exp2` it produces a number - But this signature is too specific, it holds too much information about the details of the problem - Let's erase them, make ourselves ignorant -- ``` def fuse[A, B](fromA: A => ExpStep[A], toB: ExpStep[B] => B)(a: A): B ``` ??? - Here we've just replaced all type arguments with type parameters - It can be read as follows: - Given a function that builds an `ExpStep` from `A` - And a function that reduces an `ExpStep` of `B` into a `B` - We can take an input `A` and produce a `B` - But this is still too specific, why are we looking at `ExpStep` - Can't we work with any container? -- ``` def fuse[F[_], A, B](fromA: A => F[A], toB: F[B] => B)(a: A): B ``` ??? - Here we just take any type `F` that takes a single type parameter - We build an `F` of `A` and reduce an `F` of `B` - That is quite generic, we've forgotten pretty much everything there is to know about our problem - But that's a step too far, there's too little information here - What could we possibly do with a value of type `F`? - We have no interface to work with it - We need a bit more knowledge to solve our problem - Luckily, we are already familiar with a very simplistic interface that works with types like `F` --- ## Interface ``` trait Functor[F[_]] { def map[A, B](fa: F[A])(f: A => B): F[B] } ``` ??? - That's the `Functor` type that we saw before, it lets us map inside of `F` - Given an `F` of `A` we can take a function from `A` to `B` and produce an `F` of `B` - That's the most minimal interface we could have - With that in hand, here's the new `fuse` signature: --- ## Follow the Types ``` def fuse[F[_]: Functor, A, B](fromA: A => F[A], toB: F[B] => B)(a: A): B = { {{content}} ``` .fuseBrace[```}```] ??? - It reads as: - Given an `F` which implements a `Functor`, and the types `A` and `B` - A function that builds `F` of `A` from `A`, and a function that reduces `F` of `B` to `B` - Take an `A` value and produce a `B` value - That's as ignorant as we can be, we've removed any irrelevant details from our problem - And now we can implement it - One of the bonuses of working with such abstract types, is that the solution is so constrained that we can just "follow the types" to solve it - Personally, I never seen the implementation of this function before preparing this talk - I literally followed the types to derive it - First step: we have an `A` value, and only a single consumer of `A`s - `fromA` - Let's pass it there -- val fa: F[A] = fromA(a) {{content}} ??? - Now we have an `F` of `A`, but no consumers for it - Though we do have a consumer for `F` of `B` - So we are a bit stuck - But recall that `F` implements a `Functor`, so if we had function from `A` to `B`, we could convert our `F` of `A` value - Actually we have such a function in scope -- val aToB: A => B = fuse(fromA, toB) {{content}} ??? - We can partially apply `fuse` to its first two arguments - And that's exactly a thing that consumes an `A` and returns a `B` - We can now map it over `fa` -- val fb: F[B] = fa.map(aToB) {{content}} ??? - Now we have an `F` of `B` - And there's only a single consumer for it, the `toB` function -- val b: B = toB(fb) {{content}} ??? - This is a `B` value, and exactly the desired result, which can return -- b ??? - It may be hard to believe but this function, derived by just following the types, actually achieves our goal - But before we can actually use it, we need to have a `Functor` instance for our `ExpStep` type --- ## Fusing ``` sealed trait ExpStep[+A] { def map[B](f: A => B): ExpStep[B] = this match { case AddStep(a, b) => AddStep(f(a), f(b)) case MulStep(a, b) => MulStep(f(a), f(b)) case ValStep(x) => ValStep(x) } } ``` ??? - The implementation is straightforward - We just go case by case over our datatype and apply `f` to its contents - Except `ValStep` which doesn't have anything relevant to `f`, and so we just ignore it - And now we can use our `fuse` function, like this: -- ``` val exp2 = BinaryOp(Mult, Val2(4), BinaryOp(Plus, Val2(5), Val2(1))) // 24 fuse(toExpStep, evalStep)(exp2) ``` ??? - This call actually traverses the `Exp2` tree step by step and converts it into `ExpStep` values - Then on the way up it converts the leaves into numbers and combines them on every step -- .quoteBox.fusing[ >We make the brain perfect before we <br /> blow it out. ] ??? - The fact that we could work on such an abstract level and get the right result just blows my mind - And in case you don't believe me that we are traversing the tree up and down only once - We can trace the execution of this call --- ## Tracing the Execution ``` BinaryOp(Mult, Val2(4), BinaryOp(Plus, Val2(5), Val2(1))) {{content}} ``` ??? - We replace the first level with a `MulStep` -- MulStep(Val2(4), BinaryOp(Plus, Val2(5), Val2(1))) {{content}} ??? - Then the `map` call takes us into the left sub expression, which we convert into a `ValStep` -- MulStep(ValStep(4), BinaryOp(Plus, Val2(5), Val2(1))) {{content}} ??? - Mapping into `ValStep` ignores the function, and it is automatically of type `ExpStep` of `Int` - Which we can now reduce into a number -- MulStep(4, BinaryOp(Plus, Val2(5), Val2(1))) {{content}} ??? - We now proceed to convert the right sub-tree - Which works similarly, by descending down the tree, converting each step, until we hit a `ValStep` - At which point we go back up and aggregate the resulting numbers -- MulStep(4, AddStep(Val2(5), Val2(1))) {{content}} -- MulStep(4, AddStep(ValStep(5), Val2(1))) {{content}} -- MulStep(4, AddStep(5, Val2(1))) {{content}} -- MulStep(4, AddStep(5, ValStep(1))) {{content}} -- MulStep(4, AddStep(5, 1)) {{content}} -- MulStep(4, 6) {{content}} -- 24 ??? - I find this whole thing amazing, and still have trouble believing that it just works - To conclude --- ## Ignorance is Strength - Purge as much knowledge as possible - Keep the code blissfully ignorant of its context - Use ignorance to your advantage ??? - We need to strive to remove as much specific knowledge from the code as possible - Not knowing the context in which the code is running restricts what it can do - Since it cannot use any specific details about its input to determine the result - We can use this ignorance to our advantage - Be it by determining some aspect of the implementation - Or by allowing the compiler to help us construct the code for us - And so, indeed, ignorance is strength --- .quoteBox.ignoranceIsStrength[ > All ambiguities and shades of meaning <br /> had been purged out of the words. <br /> So far as it could be achieved, a Newspeak word was simply a staccato sound expressing one clearly understood concept. ] --- ## Conclusion .slogans[ WAR IS PEACE FREEDOM IS SLAVERY IGNORANCE IS STRENGTH ] ??? - To sum up - We've seen here how each of these slogans maps into a useful programming idea - War on effects brings peace to our code - Freedom on one level of the code is slavery on another - And ignorance can be leveraged to help us reason about code, as well as help us write it --- ## Further Reading .furtherReading[ - Full code: [github.com/ncreep/1984-talk](https://github.com/ncreep/1984-talk) - War is Peace - [Monads for functional programming - Philip Wadler](http://homepages.inf.ed.ac.uk/wadler/papers/marktoberdorf/baastad.pdf) - [Typeclassopedia](https://wiki.haskell.org/Typeclassopedia) - Freedom is Slavery - [Constraints Liberate, Liberties Constrain - Rúnar Bjarnason](https://www.youtube.com/watch?v=GqmsQeSzMdw) - Ignorance is Strength - [Theorems for Free! - Philip Wadler](http://ttic.uchicago.edu/~dreyer/course/papers/wadler.pdf) - [Functional Programming with Bananas, Lenses, Envelopes and Barbed Wire - Meijer, Fokking and Paterson](http://maartenfokkinga.github.io/utwente/mmf91m.pdf) - [An Introduction to Recursion Schemes - Patrick Thomson](http://blog.sumtypeofway.com/an-introduction-to-recursion-schemes/) ] ??? - The full code for this presentation can be found here - A much better presentation on the usefulness of Monads in programming is given in Wadler's paper - And the Typeclassopedia resource contains many useful abstractions along the lines of Functors and the like - "Constraints Liberate, Liberties Constrain" is a talk by Rúnar Bjarnason that gives deeper insight on how freedom on one level is slavery on another - The idea of parametricity that I handwaved about is formalized in Wadler's article - The `fuse` function is more commonly known as a 'hylomorphism' - And it's just one of the many building blocks of the subject called "recursion schemes" - The topic of recursion schemes, was popularized in Meijer, et al's. article - The last item, which is a series of blog posts is a somewhat more accessible introduction to the topic --- class: transition, middle, future > If you want a picture of the future, imagine a boot stamping on a human face ‒ forever. .questions.centered[Questions?]